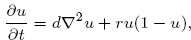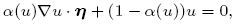Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Delgado, Manuel
Morales-Rodrigo, Cristian
Suárez, Antonio
and
Tello, J. Ignacio
2010.
On a parabolic–elliptic chemotactic model with coupled boundary conditions.
Nonlinear Analysis: Real World Applications,
Vol. 11,
Issue. 5,
p.
3884.
Goddard, Jerome
Lee, EunKyoung
and
Shivaji, R
2010.
A Double S-Shaped Bifurcation Curve for a Reaction-Diffusion Model with Nonlinear Boundary Conditions.
Boundary Value Problems,
Vol. 2010,
Issue. 1,
p.
357542.
Umezu, Kenichiro
2010.
Global bifurcation results for semilinear elliptic boundary value problems with indefinite weights and nonlinear boundary conditions.
Nonlinear Differential Equations and Applications NoDEA,
Vol. 17,
Issue. 3,
p.
323.
Cantrell, Robert S.
Cosner, Chris
and
Martínez, Salomé
2011.
Steady state solutions of a logistic equation with nonlinear boundary conditions.
Rocky Mountain Journal of Mathematics,
Vol. 41,
Issue. 2,
Hung, Kuo-Chih
Wang, Shin-Hwa
and
Yu, Chien-Hsien
2012.
Existence of a double S-shaped bifurcation curve with six positive solutions for a combustion problem.
Journal of Mathematical Analysis and Applications,
Vol. 392,
Issue. 1,
p.
40.
Goddard, Jerome
and
Shivaji, Ratnasingham
2014.
Diffusive logistic equation with constant yield harvesting and negative density dependent emigration on the boundary.
Journal of Mathematical Analysis and Applications,
Vol. 414,
Issue. 2,
p.
561.
Zhang, Yang
and
Wang, Mingxin
2014.
Bifurcation of Lotka–Volterra competition model with nonlinear boundary conditions.
Applied Mathematics Letters,
Vol. 38,
Issue. ,
p.
52.
Zhang, Yang
and
Wang, Mingxin
2015.
Bifurcation from trivial solution for elliptic systems with nonlinear boundary conditions.
Complex Variables and Elliptic Equations,
Vol. 60,
Issue. 7,
p.
951.
Kim, C.-G.
Liang, Z.-P.
and
Shi, J.-P.
2015.
Existence of positive solutions to a Laplace equation with nonlinear boundary condition.
Zeitschrift für angewandte Mathematik und Physik,
Vol. 66,
Issue. 6,
p.
3061.
Liu, Ping
and
Shi, Junping
2018.
Bifurcation of positive solutions to scalar reaction–diffusion equations with nonlinear boundary condition.
Journal of Differential Equations,
Vol. 264,
Issue. 1,
p.
425.
Kim, Chan-Gyun
and
Lee, Eun Kyoung
2018.
Existence of positive solutions to semilinear elliptic problems with nonlinear boundary condition.
Proceedings - Mathematical Sciences,
Vol. 128,
Issue. 5,
Guo, Shangjiang
2021.
Bifurcation in a reaction-diffusion model with nonlocal delay effect and nonlinear boundary condition.
Journal of Differential Equations,
Vol. 289,
Issue. ,
p.
236.
Guo, Shangjiang
2023.
Stability and bifurcation in a single species with nonlinear boundary conditions.
Proceedings of the American Mathematical Society,
Guo, Shangjiang
2023.
Behavior and Stability of Steady-State Solutions of Nonlinear Boundary Value Problems with Nonlocal Delay Effect.
Journal of Dynamics and Differential Equations,
Vol. 35,
Issue. 4,
p.
3487.
Guo, Shangjiang
2023.
Global dynamics of a Lotka-Volterra competition-diffusion system with nonlinear boundary conditions.
Journal of Differential Equations,
Vol. 352,
Issue. ,
p.
308.
Li, Zhenzhen
Dai, Binxiang
and
Zou, Xingfu
2023.
Stability and bifurcation of a reaction-diffusion-advection model with nonlinear boundary condition.
Journal of Differential Equations,
Vol. 363,
Issue. ,
p.
1.
Li, Chaochao
and
Guo, Shangjiang
2024.
Bifurcation and stability of a reaction–diffusion–advection model with nonlocal delay effect and nonlinear boundary condition.
Nonlinear Analysis: Real World Applications,
Vol. 78,
Issue. ,
p.
104089.
Ji, Quanli
Wu, Ranchao
and
Zhang, Tonghua
2024.
Dynamics of a single population model with memory and nonlinear boundary condition.
Applicable Analysis,
p.
1.