Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-12-04T19:35:45.340Z Has data issue: false hasContentIssue false
  • English
  • Français

Global bifurcation analysis and uniqueness for a semilinear problem

Published online by Cambridge University Press:  14 November 2011

Achilles Tertikas
Achilles Tertikas
Affiliation:
Department of Mathematics, Heriot-Watt University, Edinburgh EH14 4AS, U.K.
Get access Rights & Permissions [Opens in a new window]

Synopsis

We study the bifurcation diagram and uniqueness of solutions of

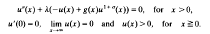
By using a rescaling technique and the Implicit Function Theorem, we establish the global bifurcation diagram. Uniqueness is proved by a separation argument to complete the bifurcation picture of the problem. Our study suggests that the bifurcation diagrams have different behaviour at λ = 0, depending on whether g(∞) > 0 or g(∞) < 0 in L∞ norm, but quite similar behaviour in Lp or W2,1.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 111 , Issue 3-4 , 1989 , pp. 265 - 284
Copyright
Copyright © Royal Society of Edinburgh 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Benci, V. and Fortunato, D.. Does bifurcation from the essential spectrum occur? Comm. Partial Differential Equations 6 (1981), 249–272.Google Scholar
2Bongers, A., Heinz, H. P. and Küpper, T.. Existence and bifurcation theorems for nonlinear elliptic eigenvalue problems on unbounded domains. J. Differential Equations 47 (1983) 327–357.Google Scholar
3Brezis, H.. Analyse fonctionelle (Paris: Masson, 1983).Google Scholar
4Chow, S. N. and Hale, J.. Methods in bifurcation theory, Grundlehren 251 (New York: Springer 1982).Google Scholar
5Gidas, B. and Spruck, J.. A priori bounds for positive solutions of nonlinear elliptic equations. Comm. Partial Differential Equations 6 (1981), 883–901.Google Scholar
6Peletier, L. A. and Serrin, J.. Uniqueness of positive solutions of semilinear equations in ℝN. Arch. Rational Mech. Anal. 81 (1983), 181–197.Google Scholar
7Protter, M. H. and Weinberger, H.. Maximum principles in differential equations (Englewood Cliffs, New Jersey: Prentice-Hall, 1967).Google Scholar
8Stuart, C. A.. A global branch of solutions to a semilinear equation on a unbounded interval. Proc. Roy. Soc. Edinburgh Sect. A 101 (1985), 273–282.Google Scholar
9Stuart, C. A.. Bifurcation in Lp(ℝ) for a semilinear equation. J. Differential.Equations 64 (1986), 294–316.Google Scholar
10Stuart, C. A.. Bifurcation from the continuous spectrum in LP(ℝ) (preprint, 1987).Google Scholar
11Toland, J. F.. Global bifurcation for Neumann problems without eigenvalues. J. Differential Equations 44 (1982), 82–110.Google Scholar
12Toland, J. F.. Uniqueness of positive solutions of some semilinear Sturm–Liouville problems on the half-line. Proc. Roy. Soc. Edinburgh Sect. A 97 (1984), 259–263.Google Scholar