Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-03T01:03:45.061Z Has data issue: false hasContentIssue false
  • English
  • Français

A generalisation of the inverse spectral theorem of Levitan and Gasymov

Published online by Cambridge University Press:  14 November 2011

Christine Thurlow
Christine Thurlow
Affiliation:
121 The Grove, Ealing, London W5
Get access Rights & Permissions [Opens in a new window]

Synopsis

In the Inverse Spectral Theorem in the form given by Levitan and Gasymov, necessary and sufficient conditions are given for a non-decreasing function, p(ℷ), to be the spectral function of a Sturm–Liouville problem. In these conditions, p(ℷ) is compared with the spectral function for the particular Strum–Liouville problem

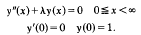
If the method of Levitan and Gasymov's proof is slightly adapted, the necessary and sufficient conditions can be stated in a more general form in which p(ℷ) is compared with the spectral function for any problem of the form

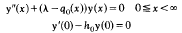
where hO is real and qo(x) locally integrable.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 84 , Issue 3-4 , 1979 , pp. 185 - 196
Copyright
Copyright © Royal Society of Edinburgh 1979

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Gelfand, I. M. and Levitan, B. M.. On the determination of a differential equation from its spectral function. Amer. Math. Soc. Transl. 1 (1955), 253–304.Google Scholar
2Levitan, B. M. and Gasymov, M. G.. Determination of a differential equation by two of its spectra. Russian Math. Surveys 19 (1964), 1–63.CrossRefGoogle Scholar
3Naïmark, M. A.. Linear differential operators, Pt 2 (New York: Ungar, 1968).Google Scholar
4Thurlow, C. R.. Topics in differential equations, (Oxford Univ. D. Phil. Thesis, 1978).Google Scholar
5Titchmarsh, E. C.. Eigenfunction expansions associated with second order differential equations, Pt 2 (Oxford Univ. Press, 1958).Google Scholar