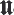Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T20:00:46.000Z Has data issue: false hasContentIssue false
  • English
  • Français

Formation theory and groups of automorphisms of -groups*

Published online by Cambridge University Press:  14 February 2012

M. J. Tomkinson
M. J. Tomkinson
Affiliation:
Department of Mathematics, University of Glasgow
Get access Rights & Permissions [Opens in a new window]

Synopsis

Further results from the theory of finite soluble groups are extended to the class 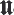of locally finite groups with a satisfactory Sylow structure. Let 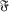be a saturated U-formation and A a 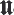-group of automorphisms of the 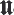-group G. A is said to act 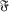-centrally on G if G has an A-composition series (Λσ/Vσ; σ ∈ ∑) such that A induces an f(p)-group of automorphisms in each p-factor Λσ/Vσ. We show that in this situation A is an 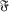-group, thus generalising the result of Schmid [8]. Associated results of Schmid and of Baer are also extended to the infinite case.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 76 , Issue 4 , 1977 , pp. 255 - 265
Copyright
Copyright © Royal Society of Edinburgh 1977

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Baer, R.. Durch Formationen bestimmte Zerlegungen von Normalteilern einer endlichen Gruppe. J. Algebra 20 (1972), 38–56.CrossRefGoogle Scholar
2Gardiner, A. D., Hartley, B. and Tomkinson, M. J.. Saturated formations and Sylow structure in locally finite groups. J. Algebra 17 (1971), 177–211.CrossRefGoogle Scholar
3Graddon, C. J.. Some generalizations to certain locally finite groups of theorems due to Chambers and Rose. Illinois J. Math. 17 (1973), 666–679.CrossRefGoogle Scholar
4Huppert, B.. Endliche Gruppen I (Berlin: Springer, 1967).CrossRefGoogle Scholar
5Huppert, B.. Zur Theorie der Formationen. Arch. Math. (Basel) 19 (1969), 561–574.CrossRefGoogle Scholar
6Robinson, D. J. S.. Finiteness Conditions and Generalized Soluble Groups, Pt 1. Ergebn. Math. 62 (1972).Google Scholar
7Schmid, P.. Formationen und Automorphismengruppen. J. London Math. Soc. 7 (1973), 83–94.Google Scholar
8Schmid, P.. Lokale Formationen endlicher Gruppen. Math. Z. 137 (1974), 31–48.Google Scholar
9Tomkinson, M. J.. A Frattini-like subgroup. Math. Proc. Cambridge Philos. Soc. 11 (1975), 247–257.CrossRefGoogle Scholar