Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T19:46:50.314Z Has data issue: false hasContentIssue false
  • English
  • Français

First-order expansions for eigenvalues and eigenfunctions in periodic homogenization

Part of: Spectral theory and eigenvalue problems Partial differential equations

Published online by Cambridge University Press:  20 March 2019

Jinping Zhuge
Jinping Zhuge*
Affiliation:
Department of Mathematics, University of Kentucky, Lexington, KY40506, USA ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

For a family of elliptic operators with periodically oscillating coefficients, 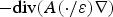$-{\rm div}(A(\cdot /\varepsilon )\nabla )$ with tiny ε > 0, we comprehensively study the first-order expansions of eigenvalues and eigenfunctions (eigenspaces) for both the Dirichlet and Neumann problems in bounded, smooth and strictly convex domains (or more general domains of finite type). A new first-order correction term is introduced to derive the expansion of eigenfunctions in L2 or 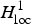$H^1_{\rm loc}$. Our results rely on the recent progress on the homogenization of boundary layer problems.

Keywords

Homogenizationeigenvalueseigenfunctionsboundary layers

MSC classification

Primary: 35B27: Homogenization; equations in media with periodic structure
Secondary: 35P20: Asymptotic distribution of eigenvalues and eigenfunctions
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 150 , Issue 5 , October 2020 , pp. 2189 - 2215
Check for updates
Copyright
Copyright © Royal Society of Edinburgh 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Allaire, G. and Conca, C.. Bloch wave homogenization and spectral asymptotic analysis. J. Math. Pures Appl. (9) 77 (1998), 153–208. MR 1614641.Google Scholar
2Armstrong, S., Kuusi, T., Mourrat, J.-C. and Prange, C.. Quantitative analysis of boundary layers in periodic homogenization. Arch. Ration. Mech. Anal. 226 (2017), 695–741. MR 3687879.CrossRefGoogle Scholar
3Gérard-Varet, D. and Masmoudi, N.. Homogenization in polygonal domains. J. Eur. Math. Soc. (JEMS) 13 (2011), 1477–1503. MR 2825170.CrossRefGoogle Scholar
4Gérard-Varet, D. and Masmoudi, N.. Homogenization and boundary layers. Acta Math. 209 (2012), 133–178. MR 2979511.CrossRefGoogle Scholar
5Kenig, C., Lin, F. and Shen, Z.. Estimates of eigenvalues and eigenfunctions in periodic homogenization. J. Eur. Math. Soc. (JEMS) 15 (2013), 1901–1925. MR 3082248.CrossRefGoogle Scholar
6Kesavan, S.. Homogenization of elliptic eigenvalue problems. I. Appl. Math. Optim. 5 (1979), 153–167. MR 533617.CrossRefGoogle Scholar
7Kesavan, S.. Homogenization of elliptic eigenvalue problems. II Appl. Math. Optim. 5 (1979), 197–216. MR 546068.CrossRefGoogle Scholar
8Moskow, S. and Vogelius, M.. First-order corrections to the homogenised eigenvalues of a periodic composite medium. A convergence proof. Proc. Roy. Soc. Edinburgh Sect. A 127 (1997), 1263–1299. MR 1489436.CrossRefGoogle Scholar
9Osborn, J. E.. Spectral approximation for compact operators. Math. Comput. 29 (1975), 712–725. MR 0383117.CrossRefGoogle Scholar
10Prange, C.. First-order expansion for the Dirichlet eigenvalues of an elliptic system with oscillating coefficients. Asymptot. Anal. 83 (2013), 207–235. MR 3112850.Google Scholar
11Santosa, F. and Vogelius, M.. First-order corrections to the homogenized eigenvalues of a periodic composite medium. SIAM J. Appl. Math. 53 (1993), 1636–1668. MR 1247172.CrossRefGoogle Scholar
12Shen, Z.. Periodic homogenization of elliptic systems. Operator theory: advances and applications, vol. 269 (Cham: Birkhäuser/Springer, 2018).Google Scholar
13Shen, Z. and Zhuge, J.. Boundary layers in periodic homogenization of Neumann problems. Comm. Pure Appl. Math. 71 (2018), 2163–2219. MR 3862089.CrossRefGoogle Scholar
14Shen, Z. and Zhuge, J.. Regularity of homogenized boundary data in periodic homogenization of elliptic systems. J. Eur. Math. Soc. (JEMS) (To appear).Google Scholar
15Zhuge, J.. Homogenization and boundary layers in domains of finite type. Comm. Partial Differ. Equ. 43 (2018), 549–584. MR 3902170.CrossRefGoogle Scholar