Families of curve congruences on Lorentzian surfaces and pencils of quadratic forms
Published online by Cambridge University Press: 03 June 2011
Abstract
We define and study families of conjugate and reflected curve congruences associated to a self-adjoint operator 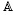 on a smooth and oriented surface M endowed with a Lorentzian metric g. These families trace parts of the pencil joining the equations of the
on a smooth and oriented surface M endowed with a Lorentzian metric g. These families trace parts of the pencil joining the equations of the 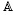 -asymptotic and the
-asymptotic and the 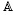 -principal curves, and the pencil joining the
-principal curves, and the pencil joining the 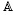 -characteristic and the
-characteristic and the 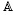 -principal curves, respectively. The binary differential equations (BDEs) of these curves can be viewed as points in the projective plane. Using the polar lines of various BDEs with respect to the conic of degenerate quadratic forms, we obtain geometric results on the above pencils and their relation with the metric g, on the type of solutions of a given BDE, of its
-principal curves, respectively. The binary differential equations (BDEs) of these curves can be viewed as points in the projective plane. Using the polar lines of various BDEs with respect to the conic of degenerate quadratic forms, we obtain geometric results on the above pencils and their relation with the metric g, on the type of solutions of a given BDE, of its 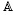 -conjugate equation and on BDEs with orthogonal roots.
-conjugate equation and on BDEs with orthogonal roots.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 141 , Issue 3 , June 2011 , pp. 655 - 672
- Copyright
- Copyright © Royal Society of Edinburgh 2011
- 3
- Cited by


