Existence of positive solutions of some semilinear elliptic equations with singular coefficients

Abstract

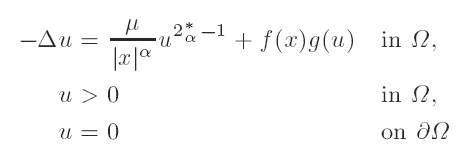In this paper we consider the semilinear elliptic problem in a bounded domain Ω ⊆ Rⁿ, where μ ≥ 0, 0 ≤ α ≤ 2, 2_α* := 2(n − α)/(n − 2), f : Ω → R⁺ is measurable, f > 0 a.e, having a lower-order singularity than |x|^-2 at the origin, and g : R → R is either linear or superlinear. For 1 < p < n, we characterize a class of singular functions I_p for which the embedding is compact. When p = 2, α = 2, f ∈ I₂ and 0 ≤ μ < (½(n − 2))², we prove that the linear problem has -discrete spectrum. By improving the Hardy inequality we show that for f belonging to a certain subclass of I₂, the first eigenvalue goes to a positive number as μ approaches (½(n − 2))². Furthermore, when g is superlinear, we show that for the same subclass of I₂, the functional corresponding to the differential equation satisfies the Palais-Smale condition if α = 2 and a Brezis-Nirenberg type of phenomenon occurs for the case 0 ≤ α < 2.