Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-01-26T14:16:50.998Z Has data issue: false hasContentIssue false
  • English
  • Français

Existence conditions for eigenvalue problems generated by compact multiparameter operators

Published online by Cambridge University Press:  14 November 2011

Paul Binding ,
Patrick J. Browne  and
Lawrence Turyn
Paul Binding
Affiliation:
Department of Mathematics and Statistics, The University of Calgary, Calgary, Alberta, CanadaT2N 1N4
Patrick J. Browne
Affiliation:
Department of Mathematics and Statistics, The University of Calgary, Calgary, Alberta, CanadaT2N 1N4
Lawrence Turyn
Affiliation:
Department of Mathematics, Wright State University, Dayton, Ohio 45435, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Synopsis

Let T, V1,…, Vk denote compact symmetric linear operators on a separable Hilbert space H, and write W(λ) = T + λ1V1 + … + λkVk, λ = (λ1, …, λk) ϵ ℝk. We study conditions on the cone

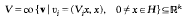
related to solubility of the multiparameter eigenvalue problem

with W(λ)−I nonpositive definite. The main result is as follows.

Theorem. If 0 ∉ V, then (*) is soluble for any T. If 0 ∈ V, then there exists T such that (*) is insoluble.

We also deduce analogous results for problems involving self-adjoint operators with compact resolvent.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 96 , Issue 3-4 , 1984 , pp. 261 - 274
Copyright
Copyright © Royal Society of Edinburgh 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Binding, P. and Browne, P. J.. Spectral properties of two-parameter eigenvalue problems. Proc. Roy. Soc. Edinburgh Sect. A 89 (1981), 157–173.CrossRefGoogle Scholar
2Binding, P., Browne, P. J. and Turyn, L.. Existence conditions for two-parameter eigenvalue problems. Proc. Roy. Soc. Edinburgh Sect. A 91 (1981), 15–30.Google Scholar
3Carmichael, R. D.. Boundary value and expansion problems; formulation of various transcendental problems. Amer. J. Math. 43 (1921), 232–270.CrossRefGoogle Scholar
4Pell, A. J.. Linear equations with two parameters. Trans. Amer. Math. Soc. 23 (1922), 198–211.Google Scholar
5Rockafellar, R. T.. Convex Analysis (Princeton: Princeton University Press, 1972).Google Scholar
6Tuyrn, L.. Sturm-Liouville problems with several parameters. J. Differential Equations 38 (1980), 239–259.CrossRefGoogle Scholar