Hostname: page-component-5cf477f64f-54txb Total loading time: 0 Render date: 2025-04-06T02:52:03.856Z Has data issue: false hasContentIssue false
  • English
  • Français

Every locally compact group is the outer automorphism group of a II1 factor

Part of: Noncompact transformation groups Ergodic theory Selfadjoint operator algebras

Published online by Cambridge University Press:  28 March 2025

Stefaan Vaes Open the ORCID record for Stefaan Vaes [Opens in a new window]
Stefaan Vaes*
Affiliation:
Department of Mathematics, KU Leuven, Celestijnenlaan 200b - box 2400, Leuven 3001, Belgium ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that every locally compact second countable group G arises as the outer automorphism group 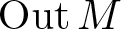$\operatorname{Out} M$ of a II1 factor, which was so far only known for totally disconnected groups, compact groups, and a few isolated examples. We obtain this result by proving that every locally compact second countable group is a centralizer group, a class of Polish groups that arise naturally in ergodic theory and that may all be realized as 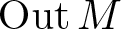$\operatorname{Out} M$.

Keywords

outer automorphism groupII1 factorvon Neumann algebradeformation/rigidity theoryPoisson suspension

MSC classification

Primary: 46L36: Classification of factors
Secondary: 46L40: Automorphisms 37A15: General groups of measure-preserving transformations 22F50: Groups as automorphisms of other structures
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 12
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Deprez, S.. Explicit examples of equivalence relations and II1 factors with prescribed fundamental group and outer automorphism group. Trans. Amer. Math. Soc. 367 (2015), 6837–6876.CrossRefGoogle Scholar
Falguières, S. and Vaes, S.. Every compact group arises as the outer automorphism group of a II1 factor. J. Funct. Anal. 254 (2008), 2317–2328.CrossRefGoogle Scholar
Ioana, A., Peterson, J. and Popa, S.. Amalgamated free products of weakly rigid factors and calculation of their symmetry groups. Acta Math. 200 (2008), 85–153.Google Scholar
Janvresse, E., Roy, E. and De La Rue, T.. Dynamical systems of probabilistic origin: Gaussian and Poisson systems, In Ergodic Theory, Encycl. Complex. Syst. Sci., pp. 217–232 (Springer, New York, 2023).Google Scholar
Popa, S. and Vaes, S.. Strong rigidity of generalized Bernoulli actions and computations of their symmetry groups. Adv. Math. 217 (2008), 833–872.Google Scholar
Popa, S. and Vaes, S.. W $^*$-rigidity paradigms for embeddings of II1 factors. Commun. Math. Phys. 395 (2022), 907–961.Google Scholar
Roy, E.. Poisson suspensions and infinite ergodic theory. Ergodic Theory Dynam. Systems 29 (2009), 667–683.CrossRefGoogle Scholar
Sutherland, C. E.. A Borel parametrization of Polish groups. Publ. Res. Inst. Math. Sci. 21 (1985), 1067–1086.Google Scholar
Vaes, S.. Explicit computations of all finite index bimodules for a family of II1 factors. Ann. Sci. éc. Norm. Supér. 41 (2008), 743–788.Google Scholar
Vaes, S. Wouters, L.. Borel fields and measured fields of Polish spaces, Banach spaces, von Neumann algebras and C $^*$-algebras. Preprint. arXiv:2405.16603.Google Scholar
Zimmer, R. J.. Ergodic theory and semisimple groups, Monogr. Math., Vol. 81 (Birkhäuser Verlag, Basel, 1984).Google Scholar