Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Keller, R. G.
1979.
The essential self-adjointness of differential operators with positive coefficients.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 82,
Issue. 3-4,
p.
345.
Kato, Tosio
1981.
Spectral Theory of Differential Operators, Proceedings of the Conference held at the University of Alabama in Birmingham.
Vol. 55,
Issue. ,
p.
253.
Dung, Nguyen Xuan
1982.
Essential self-adjointness and self-adjointness for even order elliptic operators.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 93,
Issue. 1-2,
p.
161.
Dung, Nguyen Xuan
1982.
Ordinary and Partial Differential Equations.
Vol. 964,
Issue. ,
p.
171.
Gesztesy, Fritz
Mitrea, Marius
Nenciu, Irina
and
Teschl, Gerald
2016.
Decoupling of deficiency indices and applications to Schrödinger-type operators with possibly strongly singular potentials.
Advances in Mathematics,
Vol. 301,
Issue. ,
p.
1022.
Milatovic, Ognjen
2017.
Self‐adjointness of perturbed biharmonic operators on Riemannian manifolds.
Mathematische Nachrichten,
Vol. 290,
Issue. 17-18,
p.
2948.


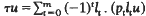 where
where 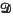 is essentially self-adjoint in
is essentially self-adjoint in 