Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Keller, R. G.
1979.
The essential self-adjointness of differential operators.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 82,
Issue. 3-4,
p.
305.
Kato, Tosio
1981.
Spectral Theory of Differential Operators, Proceedings of the Conference held at the University of Alabama in Birmingham.
Vol. 55,
Issue. ,
p.
253.


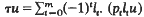 where
where 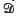 is essentially self-adjoint in
is essentially self-adjoint in 