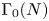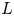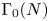1. Introduction
Let $f$![]() be any Maass cusp form (cf. [Reference Bump6]) over the congruence subgroup $\Gamma _0(N) \subset \Gamma = SL_2(\mathbb {Z})$
be any Maass cusp form (cf. [Reference Bump6]) over the congruence subgroup $\Gamma _0(N) \subset \Gamma = SL_2(\mathbb {Z})$![]() with $\Delta f = \left (\frac {1}{4}+\nu ^2\right )f$
with $\Delta f = \left (\frac {1}{4}+\nu ^2\right )f$![]() , where $\Delta$
, where $\Delta$![]() is the non-Euclidean Laplacian operator
is the non-Euclidean Laplacian operator
Since the Laplacian is self-adjoint, any eigenvalue associated with $\Delta$![]() must be a positive real number, and therefore $\nu$
must be a positive real number, and therefore $\nu$![]() is either real or of the form $it$
is either real or of the form $it$![]() with $t$
with $t$![]() real and $-1/2< t<1/2$
real and $-1/2< t<1/2$![]() .
.
We denote the Fourier coefficients of $f$![]() at cusp infinity by $\lambda _f(n)$
at cusp infinity by $\lambda _f(n)$![]() :
:
normalized by setting $\lambda _f(1)=1$![]() . Here $\lambda _f(n)$
. Here $\lambda _f(n)$![]() is then the $n$
is then the $n$![]() th Hecke eigenvalue of $f$
th Hecke eigenvalue of $f$![]() , $K_{i\nu }$
, $K_{i\nu }$![]() is the modified Bessel function of second kind, $z=x+iy$
is the modified Bessel function of second kind, $z=x+iy$![]() and $e(x) = e^{2\pi i x}$
and $e(x) = e^{2\pi i x}$![]() . The Maass cusp form $f$
. The Maass cusp form $f$![]() is said to be primitive if it is normalized cusp form which is a Hecke eigenform of all the Hecke operators.
is said to be primitive if it is normalized cusp form which is a Hecke eigenform of all the Hecke operators.
The Ramanujan conjecture asserts that $|\lambda _f(n)| = \mathcal {O}(n^\epsilon )$![]() for any positive $\epsilon$
for any positive $\epsilon$![]() . In this direction, to the best our knowledge, the best known bound for the Fourier coefficients was given by Kim and Sarnak [Reference Kim and Sarnak14], which is
. In this direction, to the best our knowledge, the best known bound for the Fourier coefficients was given by Kim and Sarnak [Reference Kim and Sarnak14], which is
for any positive $\epsilon$![]() .
.
Let $\rho : \mathbb {H} \to \mathbb {H}$![]() be the antiholomorphic involution given by $\rho (x+iy) = -x+iy$
be the antiholomorphic involution given by $\rho (x+iy) = -x+iy$![]() . We call a Maass cusp form $f$
. We call a Maass cusp form $f$![]() even if $f \circ \rho = f$
even if $f \circ \rho = f$![]() and odd if $f \circ \rho = -f$
and odd if $f \circ \rho = -f$![]() . We may attach an automorphic $L$
. We may attach an automorphic $L$![]() -function associated with the primitive Maass cusp form $f$
-function associated with the primitive Maass cusp form $f$![]() over $\Gamma _0(N)$
over $\Gamma _0(N)$![]() as
as

It has an Euler product of the form (cf. [Reference Aoki, Kanemitsu and Liu2, p. 208])

for $\textrm {Re}(s)>1$![]() , where $\chi _0$
, where $\chi _0$![]() denotes the principle character modulo $N$
denotes the principle character modulo $N$![]() . The $L$
. The $L$![]() -function $L(s,\, f)$
-function $L(s,\, f)$![]() can be analytically continued to the entire complex plane. The completed $L$
can be analytically continued to the entire complex plane. The completed $L$![]() -function associated with $f$
-function associated with $f$![]() can be defined as
can be defined as
where
Here $\epsilon$![]() takes the value $0$
takes the value $0$![]() for $f$
for $f$![]() even and $1$
even and $1$![]() for $f$
for $f$![]() odd. The completed $L$
odd. The completed $L$![]() -function $\Lambda (s,\, f)$
-function $\Lambda (s,\, f)$![]() satisfies the functional equation [Reference Aoki, Kanemitsu and Liu2, p. 208]
satisfies the functional equation [Reference Aoki, Kanemitsu and Liu2, p. 208]
where $\epsilon _f$![]() is a complex number of modulus $1$
is a complex number of modulus $1$![]() . The non-trivial zeros of $L(s,\, f)$
. The non-trivial zeros of $L(s,\, f)$![]() lie in the critical strip $0<\textrm {Re}(s)<1$
lie in the critical strip $0<\textrm {Re}(s)<1$![]() and, by the grand Riemann hypothesis, are conjectured to be on the critical line $\textrm {Re}(s) = {1}/{2}$
and, by the grand Riemann hypothesis, are conjectured to be on the critical line $\textrm {Re}(s) = {1}/{2}$![]() . The goal of this article is to obtain a transformation formula involving the non-trivial zeros of $L(s,\, f)$
. The goal of this article is to obtain a transformation formula involving the non-trivial zeros of $L(s,\, f)$![]() and to find an equivalent criterion of the grand Riemann hypothesis for $L(s,\, f)$
and to find an equivalent criterion of the grand Riemann hypothesis for $L(s,\, f)$![]() .
.
In the classical case, the problem was initiated by Ramanujan. He showed an elegant transformation formula to Hardy involving an infinite series of the Möbius function [Reference Ramanujan16, p. 312], during his stay at Trinity. Later, the identity was corrected by Hardy and Littlewood in [Reference Hardy and Littlewood12, p. 156, § 2.5], which precisely states that for $\alpha$![]() and $\beta$
and $\beta$![]() being two positive real numbers with $\alpha \beta = \pi$
being two positive real numbers with $\alpha \beta = \pi$![]() , the following identity holds:
, the following identity holds:

provided the infinite series on the right-hand side of the above equation converges where the sum is running over the non-trivial zeros $\rho$![]() of the Riemann zeta function with an assumption that the non-trivial zeros are simple. For more details, one can look into [Reference Berndt4, p. 467–468].
of the Riemann zeta function with an assumption that the non-trivial zeros are simple. For more details, one can look into [Reference Berndt4, p. 467–468].
The series on the right-hand side of (1.6) converges if we bracket the terms of the series in such a way that the terms for which
are included in the same bracket (cf. [Reference Titchmarsh20, p. 220]) but the convergence of the series is still unknown unconditionally.
The identity (1.6) leads Hardy and Littlewood [Reference Hardy and Littlewood12] to obtain an equivalent criterion of the Riemann hypothesis for $\zeta (s)$![]() , which precisely states that for the function $P(y) := \sum _{n=1}^\infty \frac {(-y)^n}{n!\zeta (2n+1)}$
, which precisely states that for the function $P(y) := \sum _{n=1}^\infty \frac {(-y)^n}{n!\zeta (2n+1)}$![]() , the bound $P(y) = \mathcal {O}(y^{-1/4+\delta })$
, the bound $P(y) = \mathcal {O}(y^{-1/4+\delta })$![]() as $y\to \infty$
as $y\to \infty$![]() for any positive $\delta$
for any positive $\delta$![]() is equivalent to the Riemann hypothesis. This equivalent criterion for the Riemann hypothesis is sometimes known as Riesz-type criterion since Riesz [Reference Riesz17] was the first mathematician to find a similar result around the same time.
is equivalent to the Riemann hypothesis. This equivalent criterion for the Riemann hypothesis is sometimes known as Riesz-type criterion since Riesz [Reference Riesz17] was the first mathematician to find a similar result around the same time.
Later, several analogues and generalizations have been investigated in different directions. For instance, a similar problem involving an extra complex variable was considered in [Reference Dixit, Roy and Zaharescu11]. The problem in the setting of Dirichlet $L$![]() -function and Dedekind zeta function has been studied in [Reference Dixit8] and [Reference Dixit, Gupta and Vatwani9] respectively. In [Reference Dixit, Roy and Zaharescu10], Dixit et al. have obtained an identity analogous to (1.6) for holomorphic Hecke eigenforms and found the similar criterion of the Riemann hypothesis for the associated $L$
-function and Dedekind zeta function has been studied in [Reference Dixit8] and [Reference Dixit, Gupta and Vatwani9] respectively. In [Reference Dixit, Roy and Zaharescu10], Dixit et al. have obtained an identity analogous to (1.6) for holomorphic Hecke eigenforms and found the similar criterion of the Riemann hypothesis for the associated $L$![]() -function. Recently, in [Reference Agarwal, Garg and Maji1], one variable generalization of (1.6) have been studied in different direction.
-function. Recently, in [Reference Agarwal, Garg and Maji1], one variable generalization of (1.6) have been studied in different direction.
We next provide the analogues of (1.6) for the non-holomorphic primitive Maass cusp form over the congruence subgroup $\Gamma _0(N)\subset \Gamma$![]() . The reciprocal of $L(s,\, f)$
. The reciprocal of $L(s,\, f)$![]() for $\textrm {Re}(s)>1$
for $\textrm {Re}(s)>1$![]() can be written as
can be written as

where

The above expression of $\widetilde {\lambda }_f(n)$![]() can be derived mainly from the Euler product of $L(s,\, f)^{-1}$
can be derived mainly from the Euler product of $L(s,\, f)^{-1}$![]() , which follows from (1.3) that
, which follows from (1.3) that

The multiplicativity of $\widetilde {\lambda }_f(n)$![]() and (1.8) together implies that for $p^m | n$
and (1.8) together implies that for $p^m | n$![]() with $m\geq 3$
with $m\geq 3$![]() , we have $\widetilde {\lambda }_f(n) = 0$
, we have $\widetilde {\lambda }_f(n) = 0$![]() . Therefore, from the fact that both $\lambda _f(n)$
. Therefore, from the fact that both $\lambda _f(n)$![]() and $\chi _0(n)$
and $\chi _0(n)$![]() are multiplicative, we obtain (1.7).
are multiplicative, we obtain (1.7).
We next define two functions

and

In the following theorem, we obtain transformation formulas involving the non-trivial zeros of $L(s,\, f)$![]() .
.
Theorem 1.1 Let $f$![]() be a normalized primitive Maass cusp form over the congruence subgroup $\Gamma _0(N)$
be a normalized primitive Maass cusp form over the congruence subgroup $\Gamma _0(N)$![]() with eigenvalue $1/4+\nu ^2$
with eigenvalue $1/4+\nu ^2$![]() . Let $L(s,\, f)$
. Let $L(s,\, f)$![]() be its associated $L$
be its associated $L$![]() -function as defined in (1.2). Let $\epsilon _f$
-function as defined in (1.2). Let $\epsilon _f$![]() be the complex number of modulus $1$
be the complex number of modulus $1$![]() appeared in (1.5). If $\alpha$
appeared in (1.5). If $\alpha$![]() and $\beta$
and $\beta$![]() are any positive numbers with $\alpha \beta = 1/N$
are any positive numbers with $\alpha \beta = 1/N$![]() . If the multiplicity of a non-trivial zero $\rho$
. If the multiplicity of a non-trivial zero $\rho$![]() of $L(s,\, f)$
of $L(s,\, f)$![]() is $n_\rho$
is $n_\rho$![]() , Then
, Then
(a) for $f$
 odd, we have
(1.11)\begin{align} & \alpha^{3/2} \mathcal{P}_{f_o} (\alpha) - \epsilon_f \beta^{3/2} \mathcal{P}_{f_o} (\beta) \nonumber\\ & \quad ={-}\frac{\epsilon_f}{4\pi}\sum_{\rho} \frac{1}{(n_\rho-1)!}\lim_{s\to\rho}\frac{{\rm d}^{n_\rho-1}}{{\rm d}s^{n_\rho-1}}\left\{\frac{(s-\rho)^{n_\rho}L_\infty(1-s,f)\beta^{s-\frac{1}{2}}}{L(s,f)}\right\}, \end{align}
odd, we have
(1.11)\begin{align} & \alpha^{3/2} \mathcal{P}_{f_o} (\alpha) - \epsilon_f \beta^{3/2} \mathcal{P}_{f_o} (\beta) \nonumber\\ & \quad ={-}\frac{\epsilon_f}{4\pi}\sum_{\rho} \frac{1}{(n_\rho-1)!}\lim_{s\to\rho}\frac{{\rm d}^{n_\rho-1}}{{\rm d}s^{n_\rho-1}}\left\{\frac{(s-\rho)^{n_\rho}L_\infty(1-s,f)\beta^{s-\frac{1}{2}}}{L(s,f)}\right\}, \end{align}
(b) for $f$
 even, we have
(1.12)\begin{align} \sqrt{\alpha} \mathcal{P}_{f_e}(\alpha) - \epsilon_f \sqrt{\beta} \mathcal{P}_{f_e}(\beta) & = \frac{\epsilon_f \pi^{i\nu}\Gamma({-}i\nu)}{L({-}i\nu,f)}\beta^{\frac{1}{2}+i\nu}+\frac{\epsilon_f \pi^{{-}i\nu}\Gamma(i\nu)}{L(i\nu,f)}\beta^{\frac{1}{2}-i\nu} \nonumber\\ & \quad-\epsilon_f\sum_\rho \frac{1}{(n_\rho-1)!}\lim_{s\to\rho}\frac{d^{n_\rho-1}}{ds^{n_\rho-1}}\nonumber\\ & \quad \times\left\{\frac{(s-\rho)^{n_\rho}L_\infty(1-s,f)\beta^{s-\frac{1}{2}}}{L(s,f)}\right\}, \end{align}
even, we have
(1.12)\begin{align} \sqrt{\alpha} \mathcal{P}_{f_e}(\alpha) - \epsilon_f \sqrt{\beta} \mathcal{P}_{f_e}(\beta) & = \frac{\epsilon_f \pi^{i\nu}\Gamma({-}i\nu)}{L({-}i\nu,f)}\beta^{\frac{1}{2}+i\nu}+\frac{\epsilon_f \pi^{{-}i\nu}\Gamma(i\nu)}{L(i\nu,f)}\beta^{\frac{1}{2}-i\nu} \nonumber\\ & \quad-\epsilon_f\sum_\rho \frac{1}{(n_\rho-1)!}\lim_{s\to\rho}\frac{d^{n_\rho-1}}{ds^{n_\rho-1}}\nonumber\\ & \quad \times\left\{\frac{(s-\rho)^{n_\rho}L_\infty(1-s,f)\beta^{s-\frac{1}{2}}}{L(s,f)}\right\}, \end{align}
provided the series on the right-hand of (1.11) and (1.12) converge where $\rho$![]() runs through the non-trivial zeros of $L(s,\, f)$
runs through the non-trivial zeros of $L(s,\, f)$![]() . In particular, if all non-trivial zeros of $L(s,\, f)$
. In particular, if all non-trivial zeros of $L(s,\, f)$![]() are simple,
are simple,
(a) for $f$
 odd, we have
(1.13)\begin{equation} \alpha^{3/2} \mathcal{P}_{f_o} (\alpha) - \epsilon_f \beta^{3/2} \mathcal{P}_{f_o} (\beta) ={-}\frac{\epsilon_f}{4\pi}\sum_{\rho} \frac{L_\infty(1-\rho, f)}{L'(\rho, f)} \beta^{\rho-\frac{1}{2}}, \end{equation}
odd, we have
(1.13)\begin{equation} \alpha^{3/2} \mathcal{P}_{f_o} (\alpha) - \epsilon_f \beta^{3/2} \mathcal{P}_{f_o} (\beta) ={-}\frac{\epsilon_f}{4\pi}\sum_{\rho} \frac{L_\infty(1-\rho, f)}{L'(\rho, f)} \beta^{\rho-\frac{1}{2}}, \end{equation}
(b) for $f$
 even, we have
(1.14)\begin{align} \sqrt{\alpha} \mathcal{P}_{f_e}(\alpha) - \epsilon_f \sqrt{\beta} \mathcal{P}_{f_e}(\beta) & = \frac{\epsilon_f \pi^{i\nu}\Gamma({-}i\nu)}{L({-}i\nu,f)}\beta^{\frac{1}{2}+i\nu} +\frac{\epsilon_f \pi^{{-}i\nu}\Gamma(i\nu)}{L(i\nu,f)}\beta^{\frac{1}{2}-i\nu}\nonumber\\& \quad -\epsilon_f\sum_\rho \frac{L_\infty(1-\rho, f)}{L'(\rho, f)} \beta^{\rho-\frac{1}{2}}. \end{align}
even, we have
(1.14)\begin{align} \sqrt{\alpha} \mathcal{P}_{f_e}(\alpha) - \epsilon_f \sqrt{\beta} \mathcal{P}_{f_e}(\beta) & = \frac{\epsilon_f \pi^{i\nu}\Gamma({-}i\nu)}{L({-}i\nu,f)}\beta^{\frac{1}{2}+i\nu} +\frac{\epsilon_f \pi^{{-}i\nu}\Gamma(i\nu)}{L(i\nu,f)}\beta^{\frac{1}{2}-i\nu}\nonumber\\& \quad -\epsilon_f\sum_\rho \frac{L_\infty(1-\rho, f)}{L'(\rho, f)} \beta^{\rho-\frac{1}{2}}. \end{align}
The next theorem provides an equivalent criterion of the grand Riemann hypothesis for $L(s,\, f)$![]() when $f$
when $f$![]() is odd, motivated from the above theorem.
is odd, motivated from the above theorem.
Theorem 1.2 If $f$![]() is an odd normalized primitive Maass cusp form over the congruence subgroup $\Gamma _0(N)$
is an odd normalized primitive Maass cusp form over the congruence subgroup $\Gamma _0(N)$![]() with eigenvalue $1/4+\nu ^2$
with eigenvalue $1/4+\nu ^2$![]() . Then the bound $\mathcal {P}_{f_o} (y) = \mathcal {O}(y^{-3/2+\delta })$
. Then the bound $\mathcal {P}_{f_o} (y) = \mathcal {O}(y^{-3/2+\delta })$![]() as $y \to \infty$
as $y \to \infty$![]() for every positive $\delta$
for every positive $\delta$![]() is equivalent to the grand Riemann hypothesis for $L(s,\, f)$
is equivalent to the grand Riemann hypothesis for $L(s,\, f)$![]() .
.
Now we consider the remaining case when $f$![]() is even. In obtaining the criterion of the grand Riemann hypothesis for $L(s,\, f)$
is even. In obtaining the criterion of the grand Riemann hypothesis for $L(s,\, f)$![]() for $f$
for $f$![]() even, we need to consider the derivative of the function $\mathcal {P}_{f_e}(y)$
even, we need to consider the derivative of the function $\mathcal {P}_{f_e}(y)$![]() , unlike to the case when $f$
, unlike to the case when $f$![]() is odd. The reason behind the above fact is technical, which is mainly due to the poles coming from the gamma factors involved in the functional equation (1.5) of $L(s,\, f)$
is odd. The reason behind the above fact is technical, which is mainly due to the poles coming from the gamma factors involved in the functional equation (1.5) of $L(s,\, f)$![]() . Let $\mathcal {Q}_{f_e} (y)$
. Let $\mathcal {Q}_{f_e} (y)$![]() be the derivative of the function $\mathcal {P}_{f_e}(y)$
be the derivative of the function $\mathcal {P}_{f_e}(y)$![]() . Thus it follows from the derivative of the K-Bessel function [Reference Brychkov5, p. 36, Formula 1.14.1.1] that
. Thus it follows from the derivative of the K-Bessel function [Reference Brychkov5, p. 36, Formula 1.14.1.1] that

Theorem 1.3 Let $f$![]() be an even normalized primitive Maass cusp form over the congruence subgroup $\Gamma _0(N)$
be an even normalized primitive Maass cusp form over the congruence subgroup $\Gamma _0(N)$![]() with eigenvalue $1/4+\nu ^2$
with eigenvalue $1/4+\nu ^2$![]() . Then
. Then
(a) The bound $\mathcal {Q}_{f_e} (y) = \mathcal {O}(y^{-3/2+\delta })$
 for any $\delta >0$
for any $\delta >0$ implies the grand Riemann hypothesis for $L(s,\, f)$
implies the grand Riemann hypothesis for $L(s,\, f)$ .
.(b) If the grand Riemann hypothesis for $L(s,\, f)$
 is true, then as $y\to \infty$
is true, then as $y\to \infty$ ,
(1.16)\begin{equation} \mathcal{Q}_{f_e} (y) ={-}\pi \sum_{n=1}^{[y^{1-\epsilon}]-1}\frac{\widetilde{\lambda}_f(n)}{n^2} \left\{ \frac{\Gamma(1+i\nu)}{(\pi y/n)^{1+i\nu}} + \frac{\Gamma(1-i\nu)}{(\pi y/n)^{1-i\nu}} \right\} + \mathcal{O}\left(y^{{-}3/2+\delta}\right) \end{equation}and
,
(1.16)\begin{equation} \mathcal{Q}_{f_e} (y) ={-}\pi \sum_{n=1}^{[y^{1-\epsilon}]-1}\frac{\widetilde{\lambda}_f(n)}{n^2} \left\{ \frac{\Gamma(1+i\nu)}{(\pi y/n)^{1+i\nu}} + \frac{\Gamma(1-i\nu)}{(\pi y/n)^{1-i\nu}} \right\} + \mathcal{O}\left(y^{{-}3/2+\delta}\right) \end{equation}and \[ \mathcal{P}_{f_e} (y) ={-} \sum_{n=1}^{[y^{1-\epsilon}]-1}\frac{\widetilde{\lambda}_f(n)}{n} \left\{ \frac{\Gamma(i\nu)}{(\pi y/n)^{i\nu}} + \frac{\Gamma({-}i\nu)}{(\pi y/n)^{{-}i\nu}} \right\} + \mathcal{O}\left(y^{{-}1/2+\delta}\right). \]
\[ \mathcal{P}_{f_e} (y) ={-} \sum_{n=1}^{[y^{1-\epsilon}]-1}\frac{\widetilde{\lambda}_f(n)}{n} \left\{ \frac{\Gamma(i\nu)}{(\pi y/n)^{i\nu}} + \frac{\Gamma({-}i\nu)}{(\pi y/n)^{{-}i\nu}} \right\} + \mathcal{O}\left(y^{{-}1/2+\delta}\right). \]
The article is organized as follows. The next section is devoted to obtaining the transformation formulas of $L(s,\, f)$![]() . We prove the criterion for the grand Riemann hypothesis for $L(s,\, f)$
. We prove the criterion for the grand Riemann hypothesis for $L(s,\, f)$![]() for both odd and even case in § 3 and § 4, respectively.
for both odd and even case in § 3 and § 4, respectively.
2. Transformation formula involving the non-trivial zeros of $L(s,\, f)$
In this section, we obtain an analogous result of (1.6) in the setting of primitive Maass cusp form. In the following lemma, we provide a lower bound for $L(s,\, f)$![]() which will be used to prove theorem 1.1.
which will be used to prove theorem 1.1.
Lemma 2.1 For a sequence of positive numbers $T$![]() as $T\to \infty$
as $T\to \infty$![]() through values such that $|T-\gamma | > \exp (-A_1\gamma /\log \gamma )$
through values such that $|T-\gamma | > \exp (-A_1\gamma /\log \gamma )$![]() for every ordinate $\gamma$
for every ordinate $\gamma$![]() of a zero of $L(s,\, f)$
of a zero of $L(s,\, f)$![]() , where $A_1$
, where $A_1$![]() is sufficiently small positive constant, the bound
is sufficiently small positive constant, the bound
holds for $\sigma \in [-1/2,\, 3/2]$![]() , where $0< A_2<\frac {\pi }{4}$
, where $0< A_2<\frac {\pi }{4}$![]() .
.
Proof. The key ingredients to prove the above lemma are followed from [Reference Iwaniec and Kowalski13, p. 102, Formula 5.24] and [Reference Sankaranarayanan and Sengupta18, Lemma 3.6]. One can therefore apply a similar argument as in [Reference Titchmarsh20, p. 219, § 9.8] or [Reference Dixit, Gupta and Vatwani9, p. 6] to complete the proof.
We next provide the proof of theorem 1.1 only for the case when $f$![]() odd since the proof for $f$
odd since the proof for $f$![]() even goes along the similar direction.
even goes along the similar direction.
2.1 Proof of theorem 1.1
The inverse Mellin transform of the modified Bessel function $K_{\mu }(x)$![]() [Reference Temme19, p. 253, Formula 10.32.13] is given by
[Reference Temme19, p. 253, Formula 10.32.13] is given by
which is valid for any $c >\pm \mathrm {Re}(\mu )$![]() . Here and throughout the article, $\int _{(c)}$
. Here and throughout the article, $\int _{(c)}$![]() denotes the integral $\int _{c-i\infty }^{c+i\infty }$
denotes the integral $\int _{c-i\infty }^{c+i\infty }$![]() . Replacing $s$
. Replacing $s$![]() by $s+1$
by $s+1$![]() in (2.1) and letting $x=2\pi \alpha /n$
in (2.1) and letting $x=2\pi \alpha /n$![]() and $\mu =i\nu$
and $\mu =i\nu$![]() , we have
, we have
for $-\frac {1}{2}< c<-\frac {7}{64}$![]() , where $L_\infty (s,\,f)$
, where $L_\infty (s,\,f)$![]() is defined in (1.4) for $f$
is defined in (1.4) for $f$![]() odd. We next insert (2.2) into (1.9) to obtain
odd. We next insert (2.2) into (1.9) to obtain

where in the last step we have interchanged the order of summation and integration. The functional equation of $L(s,\, f)$![]() , as in (1.5) thus yields
, as in (1.5) thus yields

We next shift the line of integration from $\textrm {Re}(s) = c$![]() to $\textrm {Re}(s) = \lambda$
to $\textrm {Re}(s) = \lambda$![]() where $1<\lambda <\frac {3}{2}$
where $1<\lambda <\frac {3}{2}$![]() . Consider the positively oriented contour formed by the line segments $[\lambda -iT,\,\lambda +iT],\, [\lambda +iT,\,c+iT],\,\ [c+iT,\,c-iT]$
. Consider the positively oriented contour formed by the line segments $[\lambda -iT,\,\lambda +iT],\, [\lambda +iT,\,c+iT],\,\ [c+iT,\,c-iT]$![]() and $[c-it,\,\lambda -iT]$
and $[c-it,\,\lambda -iT]$![]() , where T is any positive real number. Clearly, the poles of the Gamma factors in $L_\infty (1-s,\, f)$
, where T is any positive real number. Clearly, the poles of the Gamma factors in $L_\infty (1-s,\, f)$![]() are on the right side of the line $\textrm {Re}(s) = \lambda$
are on the right side of the line $\textrm {Re}(s) = \lambda$![]() . Thus, the only poles inside the contour are arising from the non-trivial zeros $\rho$
. Thus, the only poles inside the contour are arising from the non-trivial zeros $\rho$![]() of $L(s,\, f)$
of $L(s,\, f)$![]() . Therefore, by invoking the Cauchy residue theorem, we arrive at
. Therefore, by invoking the Cauchy residue theorem, we arrive at

where $R_\rho$![]() denotes a residual term at a non-trivial zero $\rho$
denotes a residual term at a non-trivial zero $\rho$![]() of $L(s,\, f)$
of $L(s,\, f)$![]() . If we assume the multiplicity of a non-trivial zero $\rho$
. If we assume the multiplicity of a non-trivial zero $\rho$![]() of $L(s,\, f)$
of $L(s,\, f)$![]() as $n_\rho$
as $n_\rho$![]() , then the residual term $R_\rho$
, then the residual term $R_\rho$![]() can be calculated as
can be calculated as

We can bind $\Gamma (s)$![]() for $s=\sigma +it$
for $s=\sigma +it$![]() , in any vertical strip using Stirling's formula, which is given by (cf. [Reference Copson7, p. 224])
, in any vertical strip using Stirling's formula, which is given by (cf. [Reference Copson7, p. 224])
Now, lemma 2.1 and (2.6) together implies that as $T\to \infty$![]() ,
,
where $A_2 < \pi /4$![]() . Therefore, the horizontal integrals in (2.5) vanishes as $T\to \infty$
. Therefore, the horizontal integrals in (2.5) vanishes as $T\to \infty$![]() . We next concentrate on the vertical integral in (2.5) and denote the vertical integral as $\mathcal {V}$
. We next concentrate on the vertical integral in (2.5) and denote the vertical integral as $\mathcal {V}$![]() . Substituting $s$
. Substituting $s$![]() by $1-s$
by $1-s$![]() and applying the relation $\alpha \beta = 1/N$
and applying the relation $\alpha \beta = 1/N$![]() respectively, the vertical integral $\mathcal {V}$
respectively, the vertical integral $\mathcal {V}$![]() reduces to
reduces to
Clearly $-\frac {1}{2}<1-\lambda <0$![]() . Therefore as $T \to \infty$
. Therefore as $T \to \infty$![]() , we can apply (2.3) to evaluate the vertical integral $\mathcal {V}$
, we can apply (2.3) to evaluate the vertical integral $\mathcal {V}$![]() as
as
Combining (2.4), (2.5) and (2.7) together, we have

Finally, we multiply both sides of the above equation by $\frac {\epsilon _f\sqrt {N\alpha }}{4\pi }$![]() and invoke the relation $\alpha \beta =1/N$
and invoke the relation $\alpha \beta =1/N$![]() to conclude the first part (1.11) of our theorem.
to conclude the first part (1.11) of our theorem.
For the second part, when $f$![]() is even, one can first apply Cauchy residue theorem in (2.1) by shifting the line of integration from $c$
is even, one can first apply Cauchy residue theorem in (2.1) by shifting the line of integration from $c$![]() to $\lambda$
to $\lambda$![]() such that $-1 < \lambda < - \frac {1}{2}$
such that $-1 < \lambda < - \frac {1}{2}$![]() and substitute $x= \frac {2\pi \alpha }{n}$
and substitute $x= \frac {2\pi \alpha }{n}$![]() , $\mu = i \nu$
, $\mu = i \nu$![]() to obtain
to obtain

Next, one can argue along a similar direction as was shown for part (a) to complete the proof of (1.12).
In particular, if all the non-trivial zeros of $L(s,\, f)$![]() are simple, the term $R_\rho$
are simple, the term $R_\rho$![]() in (2.5) can be evaluated as
in (2.5) can be evaluated as
where in the last step we applied the relation $\alpha \beta = 1/N$![]() . This completes the proof of the theorem.
. This completes the proof of the theorem.
3. Equivalent criterion for grand Riemann hypothesis when $f$ is odd
is odd
We first provide a heuristic stemming from theorem 1.1, which motivates us to get an equivalent criterion of the grand Riemann hypothesis for $L(s,\, f)$![]() . Invoking lemma 3.1 in (1.9), we obtain
. Invoking lemma 3.1 in (1.9), we obtain
as $\alpha \to 0$![]() . We now assume the grand Riemann hypothesis for $L(s,\, f)$
. We now assume the grand Riemann hypothesis for $L(s,\, f)$![]() and the convergence of the series $\sum _{\rho }\frac {L_\infty (1-\rho,\,f)}{L'(\rho,\,f)}\beta ^{\rho -\frac {1}{2}}$
and the convergence of the series $\sum _{\rho }\frac {L_\infty (1-\rho,\,f)}{L'(\rho,\,f)}\beta ^{\rho -\frac {1}{2}}$![]() . Then (1.13) and (3.1) together conclude
. Then (1.13) and (3.1) together conclude
as $\beta \to \infty$![]() .
.
The heuristic assumes the convergence of the series $\sum _{\rho }\frac {L_\infty (1-\rho,\,f)}{L'(\rho,\,f)}\beta ^{\rho -\frac {1}{2}}$![]() . It has been shown in theorem 1.2 that the assumption of the grand Riemann hypothesis is enough to obtain the bound $\mathcal {P}_{f_o}(\beta )=\mathcal {O}(\beta ^{-3/2+\delta })$
. It has been shown in theorem 1.2 that the assumption of the grand Riemann hypothesis is enough to obtain the bound $\mathcal {P}_{f_o}(\beta )=\mathcal {O}(\beta ^{-3/2+\delta })$![]() , for any $\delta >0$
, for any $\delta >0$![]() .
.
In the following lemma, we provide a bound for the function $\mathcal {P}_{f_o}(y)$![]() as $y \to 0$
as $y \to 0$![]() .
.
Lemma 3.1 Let $-\frac {1}{2}< c<-\frac {7}{64}$![]() . We have
. We have
as $y\to 0$![]() .
.
Proof. We first apply both (2.2) and (2.6) to obtain that for $-\frac {1}{2}< c<-\frac {7}{64}$![]() ,
,
Therefore, (1.9) and (3.2) imply that

where in the last step we used the convergence of the series $\sum _{n=1}^\infty \frac {\widetilde {\lambda }_f(n)}{n^{1-c}}$![]() for $-\frac {1}{2}< c<-\frac {7}{64}$
for $-\frac {1}{2}< c<-\frac {7}{64}$![]() .
.
We next obtain the Mellin transform of the function $\mathcal {P}_{f_o}(y)$![]() , which plays an important role to prove theorem 1.2, when $f$
, which plays an important role to prove theorem 1.2, when $f$![]() is odd.
is odd.
Lemma 3.2 For any complex number $s$![]() with $0<\mathrm {Re}(s)<\frac {1}{2}$
with $0<\mathrm {Re}(s)<\frac {1}{2}$![]() , we have
, we have
Proof. Let
We first make the change of variable $y$![]() to $x/n$
to $x/n$![]() and then multiply both sides by $\lambda _f(n)/n$
and then multiply both sides by $\lambda _f(n)/n$![]() to write the above integral as
to write the above integral as
Summing over $n$![]() from $1$
from $1$![]() to $\infty$
to $\infty$![]() , we interchange the order of summation and integration by applying the Weierstrass M-test and the Lebesgue dominated convergence theorem to obtain
, we interchange the order of summation and integration by applying the Weierstrass M-test and the Lebesgue dominated convergence theorem to obtain

It follows from the integral representation of $\mathcal {P}_{f_o}(y)$![]() as in (2.3) that for any $c \in \left (-\frac {1}{2},\, 0\right )$
as in (2.3) that for any $c \in \left (-\frac {1}{2},\, 0\right )$![]() , we have
, we have

where in the last step we interchanged the order of summation and integration and used the series definition of $L(s,\, f)$![]() . Therefore, substituting $\alpha$
. Therefore, substituting $\alpha$![]() by $nx$
by $nx$![]() in expression (2.2), the above series reduces to
in expression (2.2), the above series reduces to

Finally, we insert (3.4) into (3.3) and apply the Mellin transform of $K$![]() -Bessel function for $0<\textrm {Re}(s)<\frac {1}{2}$
-Bessel function for $0<\textrm {Re}(s)<\frac {1}{2}$![]() to conclude that
to conclude that
This completes the proof of our lemma.
We are now ready to prove an equivalent criterion of the grand Riemann hypothesis for $L(s,\, f)$![]() when $f$
when $f$![]() is odd.
is odd.
3.1 Proof of theorem 1.2
We first prove the sufficient condition of the grand Riemann hypothesis for $L(s,\,f)$![]() and for that we assume that the bound $\mathcal {P}_{f_o}(y)=\mathcal {O}(y^{-\frac {3}{2}+\delta })$
and for that we assume that the bound $\mathcal {P}_{f_o}(y)=\mathcal {O}(y^{-\frac {3}{2}+\delta })$![]() holds for any $\delta >0$
holds for any $\delta >0$![]() , as $y\to \infty$
, as $y\to \infty$![]() . It is already known from lemma 3.2 that the identity
. It is already known from lemma 3.2 that the identity
holds in $0<\textrm {Re}(s)<\frac {1}{2}$![]() . We claim that the identity is also valid inside the region $-\frac {1}{2}<\mathrm {Re}(s)\leq 0$
. We claim that the identity is also valid inside the region $-\frac {1}{2}<\mathrm {Re}(s)\leq 0$![]() under the assumption of the above bound of $\mathcal {P}_{f_o}(y)$
under the assumption of the above bound of $\mathcal {P}_{f_o}(y)$![]() .
.
To prove the claim, we first split the integral in the above identity into two parts, one from $0$![]() to $1$
to $1$![]() and another from $1$
and another from $1$![]() to $\infty$
to $\infty$![]() . Lemma 3.1 yields the convergence of the first integral inside the region $-\frac {1}{2}<\mathrm {Re}(s)\leq 0$
. Lemma 3.1 yields the convergence of the first integral inside the region $-\frac {1}{2}<\mathrm {Re}(s)\leq 0$![]() . It follows from the bound $\mathcal {P}_{f_o}(y)=\mathcal {O}(y^{-\frac {3}{2}+\delta })$
. It follows from the bound $\mathcal {P}_{f_o}(y)=\mathcal {O}(y^{-\frac {3}{2}+\delta })$![]() that the second integral also converges inside the same region. Therefore, the result [Reference Temme19, theorem 3.2, p. 30] implies that the integral $\int _0^\infty y^{-s}\mathcal {P}_{f_o}(y)\,{\rm d}y$
that the second integral also converges inside the same region. Therefore, the result [Reference Temme19, theorem 3.2, p. 30] implies that the integral $\int _0^\infty y^{-s}\mathcal {P}_{f_o}(y)\,{\rm d}y$![]() represents an analytic function in $-\frac {1}{2}<\mathrm {Re}(s)\leq 0$
represents an analytic function in $-\frac {1}{2}<\mathrm {Re}(s)\leq 0$![]() . The gamma factors on the right-hand side of (3.5) are also analytic inside $-\frac {1}{2}<\mathrm {Re}(s)\leq 0$
. The gamma factors on the right-hand side of (3.5) are also analytic inside $-\frac {1}{2}<\mathrm {Re}(s)\leq 0$![]() and $L(s+1,\, f)$
and $L(s+1,\, f)$![]() is entire. Therefore, the principle of analytic continuation yields our claim.
is entire. Therefore, the principle of analytic continuation yields our claim.
Now the right-hand side of (3.5) has no zeros in $-\frac {1}{2}<\mathrm {Re}(s)\leq 0$![]() . On the other hand, the integral on the left-hand side is analytic inside the same region. Therefore, $L(s+1,\, f)$
. On the other hand, the integral on the left-hand side is analytic inside the same region. Therefore, $L(s+1,\, f)$![]() does not vanish in $-\frac {1}{2}<\mathrm {Re}(s)\leq 0$
does not vanish in $-\frac {1}{2}<\mathrm {Re}(s)\leq 0$![]() which concludes that the grand Riemann hypothesis is true.
which concludes that the grand Riemann hypothesis is true.
We next prove the converse part and for that we first assume that the grand Riemann hypothesis is true. Under the assumption of the grand Riemann hypothesis for $L(s,\, f)$![]() , it follows from [Reference Iwaniec and Kowalski13, proposition 5.14, p. 113] that as $x \to \infty$
, it follows from [Reference Iwaniec and Kowalski13, proposition 5.14, p. 113] that as $x \to \infty$![]() ,
,
where $\delta$![]() is any positive real number. Let
is any positive real number. Let

Applying the Euler's partial summation formula, the above function can be bounded as
Let $\ell =\lfloor y^{1-\delta }\rfloor$![]() . We split the sum $\mathcal {P}_{f_o}(y)$
. We split the sum $\mathcal {P}_{f_o}(y)$![]() into two parts as
into two parts as
where

and

We first estimate $S_2(f,\,y)$![]() . We have
. We have

where the last term vanishes as $N\to \infty$![]() . Therefore, the above equation implies
. Therefore, the above equation implies

We next estimate the above sum by utilizing the mean value theorem and for that we define
Invoking (2.2) into (3.9), we obtain
where $-\frac {1}{2}< c <0$![]() . We differentiate $g(x)$
. We differentiate $g(x)$![]() with respect to $x$
with respect to $x$![]() and apply Stirling's formula (2.6) on the gamma factors to derive that
and apply Stirling's formula (2.6) on the gamma factors to derive that
It follows from the mean value theorem that there exists $\lambda _n\in (n,\,n+1)$![]() such that $g(n)-g(n+1)=-g'(\lambda _n)$
such that $g(n)-g(n+1)=-g'(\lambda _n)$![]() . Therefore, the sum $S_2(f,\, y)$
. Therefore, the sum $S_2(f,\, y)$![]() in (3.8) can be written as
in (3.8) can be written as

Inserting the bounds from (3.6) and (3.10) into the above equation, we arrive at

where in the penultimate step we have used the fact that $\sum _{n>x} n^{-s} = \mathcal {O}(x^{1-s})$![]() (cf. [Reference Apostol3, p. 55, theorem 3.2(c)]) and in the last step, we put $\ell =\lfloor y^{1-\delta }\rfloor$
(cf. [Reference Apostol3, p. 55, theorem 3.2(c)]) and in the last step, we put $\ell =\lfloor y^{1-\delta }\rfloor$![]() .
.
Next, we will concentrate on $S_1(f,\,y)$![]() . Utilizing the asymptotics of $K_{i\nu }(z)$
. Utilizing the asymptotics of $K_{i\nu }(z)$![]() as $z \to \infty$
as $z \to \infty$![]() [15, Formula 10.40.2, p. 255], we can bound $S_1(f,\,y)$
[15, Formula 10.40.2, p. 255], we can bound $S_1(f,\,y)$![]() as
as

Therefore, the bound of $\widetilde {\lambda }_f(n)$![]() , followed from (1.1) and the value $\ell =\lfloor y^{1-\delta }\rfloor$
, followed from (1.1) and the value $\ell =\lfloor y^{1-\delta }\rfloor$![]() , yields
, yields

for any $\delta > 0$![]() . Combining the estimates of $S_1(f,\,y)$
. Combining the estimates of $S_1(f,\,y)$![]() and $S_2(f,\,y)$
and $S_2(f,\,y)$![]() as in (3.12) and (3.11) respectively into (3.7), we can conclude that as $y\to \infty$
as in (3.12) and (3.11) respectively into (3.7), we can conclude that as $y\to \infty$![]() , $\mathcal {P}_{f_o}(y)=\mathcal {O}(y^{-\frac {3}{2}+\delta })$
, $\mathcal {P}_{f_o}(y)=\mathcal {O}(y^{-\frac {3}{2}+\delta })$![]() for any $\delta >0$
for any $\delta >0$![]() . This completes the proof of theorem 1.2(a).
. This completes the proof of theorem 1.2(a).
4. Equivalent criterion for grand Riemann hypothesis when $f$ is even
is even
In this section, we provide a criterion of the grand Riemann hypothesis for $L(s,\, f)$![]() when $f$
when $f$![]() is even, which is motivated from theorem 1.1(b). Under the assumption of the grand Riemann hypothesis for $L(s,\, f)$
is even, which is motivated from theorem 1.1(b). Under the assumption of the grand Riemann hypothesis for $L(s,\, f)$![]() and the convergence of the series $\sum _{\rho }\frac {L_\infty (1-\rho,\,f)}{L'(\rho,\,f)}\beta ^{\rho -\frac {1}{2}}$
and the convergence of the series $\sum _{\rho }\frac {L_\infty (1-\rho,\,f)}{L'(\rho,\,f)}\beta ^{\rho -\frac {1}{2}}$![]() , it follows from a similar argument in the beginning of § 3 that as $\alpha \to 0$
, it follows from a similar argument in the beginning of § 3 that as $\alpha \to 0$![]() , or equivalently, as $\beta \to \infty$
, or equivalently, as $\beta \to \infty$![]() ,
,
The heuristic is true under the assumption of the convergence of the series $\sum _{\rho }\frac {L_\infty (1-\rho,\,f)}{L'(\rho,\,f)}\beta ^{\rho -\frac {1}{2}}$![]() but without this assumption, it is shown in theorem 1.2 that the estimate of $\mathcal {P}_{f_e}(\beta )$
but without this assumption, it is shown in theorem 1.2 that the estimate of $\mathcal {P}_{f_e}(\beta )$![]() provides the main term of order $\beta ^{|i\nu |}$
provides the main term of order $\beta ^{|i\nu |}$![]() and the error term of the order $\beta ^{-1/2+\delta }$
and the error term of the order $\beta ^{-1/2+\delta }$![]() for any $\delta >0$
for any $\delta >0$![]() . As mentioned earlier in section § 1, we need to consider $\mathcal {Q}_{f_e}(\beta )$
. As mentioned earlier in section § 1, we need to consider $\mathcal {Q}_{f_e}(\beta )$![]() to find the criterion of the grand Riemann hypothesis for $L(s,\, f)$
to find the criterion of the grand Riemann hypothesis for $L(s,\, f)$![]() .
.
In order to prove the sufficient condition of the grand Riemann hypothesis, the following two lemmas are crucial.
Lemma 4.1 Let $-\frac {3}{2}< c<-\frac {1}{2}$![]() . Then for any $y>0$
. Then for any $y>0$![]() ,
,
Proof. We first consider the function
The above function can be written as

where in the penultimate step we have applied (2.8). Invoking Stirling formula for gamma functions in the above integral, we obtain
Therefore, the definition of $\mathcal {Q}_{f_e}(y)$![]() together with (4.3) yields
together with (4.3) yields

where in the last step we used the fact that the series $\sum _{n=1}^\infty \frac {\widetilde {\lambda }_f(n)}{n^{1-c}}$![]() converges as $-\frac {3}{2}< c<-\frac {1}{2}$
converges as $-\frac {3}{2}< c<-\frac {1}{2}$![]() . This proves the lemma.
. This proves the lemma.
In the following lemma, we provide the Mellin transform of $\mathcal {Q}_{f_e}(y)$![]() , which plays an important role to prove the sufficient condition of the grand Riemann hypothesis for $L(s,\,f)$
, which plays an important role to prove the sufficient condition of the grand Riemann hypothesis for $L(s,\,f)$![]() , when $f$
, when $f$![]() is even.
is even.
Lemma 4.2 For any complex number $s$![]() with $\frac {1}{2}<\mathrm {Re}(s)<\frac {3}{2}$
with $\frac {1}{2}<\mathrm {Re}(s)<\frac {3}{2}$![]() , we have
, we have
Proof. Proceeding similarly as was done in the proof of lemma 3.2, we can obtain
We finally perform the integration by parts and utilize the fact that $\mathcal {Q}_{f_e}(y) = \frac {{\rm d}}{{\rm d}y} \mathcal {P}_{f_e}(y)$![]() to conclude our lemma.
to conclude our lemma.
4.1 Proof of theorem 1.3
We first prove part (a) and for that we assume the bound $\mathcal {Q}_{f_e} (y) = \mathcal {O}(y^{-3/2+\delta })$![]() for any $\delta >0$
for any $\delta >0$![]() . Multiplying both sides of (4.4) with $(\frac {s^2+\nu ^2}{4})$
. Multiplying both sides of (4.4) with $(\frac {s^2+\nu ^2}{4})$![]() , the identity
, the identity
holds for $\frac {1}{2}<\mathrm {Re}(s)<\frac {3}{2}$![]() . Invoking lemma 4.1 and the bound of $\mathcal {Q}_{f_e} (y)$
. Invoking lemma 4.1 and the bound of $\mathcal {Q}_{f_e} (y)$![]() , it can be shown by a similar argument of the proof of theorem 1.2 that the identity is also valid inside the region $-\frac {1}{2}<\mathrm {Re}(s)<\frac {3}{2}$
, it can be shown by a similar argument of the proof of theorem 1.2 that the identity is also valid inside the region $-\frac {1}{2}<\mathrm {Re}(s)<\frac {3}{2}$![]() .
.
Now, the right-hand side of (4.5) has no zeros in $-\frac {1}{2}<\mathrm {Re}(s)<0$![]() . On the other hand, integral is also analytic inside the same region. Therefore, $L(s+1,\,f)$
. On the other hand, integral is also analytic inside the same region. Therefore, $L(s+1,\,f)$![]() has no zeros in $-\frac {1}{2}<\mathrm {Re}(s)<0$
has no zeros in $-\frac {1}{2}<\mathrm {Re}(s)<0$![]() . This completes the proof of the grand Riemann hypothesis.
. This completes the proof of the grand Riemann hypothesis.
We next prove part (b) and for that we assume the grand Riemann hypothesis for $L(s,\, f)$![]() . The argument to prove the estimates of $\mathcal {P}_{f_e} (y)$
. The argument to prove the estimates of $\mathcal {P}_{f_e} (y)$![]() and $\mathcal {Q}_{f_e} (y)$
and $\mathcal {Q}_{f_e} (y)$![]() are similar, we here provide the proof for $\mathcal {Q}_{f_e} (y)$
are similar, we here provide the proof for $\mathcal {Q}_{f_e} (y)$![]() .
.
It follows from [Reference Iwaniec and Kowalski13, proposition 5.14, p. 113] that the grand Riemann hypothesis for $L(s,\, f)$![]() implies
implies
as $x \to \infty$![]() , where $\delta$
, where $\delta$![]() is any positive real number. Let
is any positive real number. Let

Applying the Euler's partial summation formula, the above function can be bounded as
Inserting $\Omega _\nu (y,\,x)$![]() from (4.1) into the definition of $\mathcal {Q}_{f_e} (y)$
from (4.1) into the definition of $\mathcal {Q}_{f_e} (y)$![]() in (1.15), we have
in (1.15), we have

Let $\ell =\lfloor y^{1-\delta }\rfloor$![]() . We next split the above sum into two parts as
. We next split the above sum into two parts as

We first evaluate $T_2(f,\,y)$![]() . We have
. We have

Note that the last term in the above equation vanishes as $N\to \infty$![]() , therefore, we obtain
, therefore, we obtain

The mean value theorem implies that there exists $\lambda _n\in (n,\,n+1)$![]() such that
such that
We next find the estimate for the expression on the right-hand side of the above equation. Differentiating both sides of (4.2) with respect to $x$![]() , we arrive at
, we arrive at
The combination of (4.6), (4.8), (4.9) and (4.10) together with $\ell =\lfloor y^{1-\epsilon }\rfloor$![]() , yields
, yields

where in the last step we used the fact $\sum _{n>x}n^{-s}=\mathcal {O}(x^{1-s})$![]() (cf. [Reference Apostol3, p. 55, theorem 3.2(c)]).
(cf. [Reference Apostol3, p. 55, theorem 3.2(c)]).
We now estimate $T_1(f,\,y)$![]() . Invoking the estimate of $K_{z}(x)$
. Invoking the estimate of $K_{z}(x)$![]() from [15, p. 255, Formula 10.40.2], we arrive at
from [15, p. 255, Formula 10.40.2], we arrive at

Therefore, the bound of $\widetilde {\lambda }_f(n)$![]() , followed from (1.1) and the value $\ell =\lfloor y^{1-\delta }\rfloor$
, followed from (1.1) and the value $\ell =\lfloor y^{1-\delta }\rfloor$![]() , yields
, yields

for any $\delta > 0$![]() . Thus combining (4.7), (4.11) and (4.12), we conclude (1.16). This completes the proof of our theorem.
. Thus combining (4.7), (4.11) and (4.12), we conclude (1.16). This completes the proof of our theorem.
Acknowledgements
The authors would like to thank the anonymous referee for his/her valuable suggestions and comments. They also would like to show their sincere gratitude to Professor Atul Dixit for fruitful discussions and suggestions in the manuscript. The first author is an INSPIRE Faculty at IISER Kolkata funded by the grant IFA21-MA 159 of DST, Govt. of India and partially supported by SERB (NPDF) grant PDF/2021/001224. The second author's research was partially supported by the grant IBS-R003-D1 of the IBS-CGP, POSTECH, South Korea and the Fulbright-Nehru Postdoctoral Fellowship Grant 2846/FNPDR/2022.