Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-28T05:25:14.011Z Has data issue: false hasContentIssue false
  • English
  • Français

Embeddings for the space 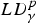$LD_\gamma ^{p}$ on sets of finite perimeter

Published online by Cambridge University Press:  07 May 2019

Nikolai V. Chemetov  and
Anna L. Mazzucato
Nikolai V. Chemetov
Affiliation:
Departamento de Matemática, Universidade Federal do Amazonas, Av. Rodrigo Octávio 6200, 69080-900Manaus, Amazonas, Brazil ([email protected])
Anna L. Mazzucato
Affiliation:
Penn State University, University Park, PA16802, USA ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Given an open set with finite perimeter $\Omega \subset {\open R}^n$, we consider the space 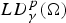$LD_\gamma ^{p}(\Omega )$, 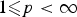$1\les p<\infty $, of functions with pth-integrable deformation tensor on Ω and with pth-integrable trace value on the essential boundary of Ω. We establish the continuous embedding 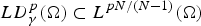$LD_\gamma ^{p}(\Omega )\subset L^{pN/(N-1)}(\Omega )$. The space 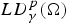$LD_\gamma ^{p}(\Omega )$ and this embedding arise naturally in studying the motion of rigid bodies in a viscous, incompressible fluid.

Keywords

Finite perimeterintegrable deformationtraceessential boundarySobolev embeddingfluid–structure interaction
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 150 , Issue 5 , October 2020 , pp. 2442 - 2461
Check for updates
Copyright
Copyright © Royal Society of Edinburgh 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Acosta, G., Armentano, M. G., Durán, R. G. and Lombardi, A. L.. Non-homogeneous Neumann problem for the Poisson equation in domains with an external cusp. J. Math. Anal. Appl. 310 (2005), 397–411.CrossRefGoogle Scholar
2Acosta, G., Durán, R. G. and López García, F.. Korn inequality and divergence operator: counterexamples and optimality of weighted estimates. Proc. Amer. Math. Soc. 141 (2013), 217–232.CrossRefGoogle Scholar
3Adams, R.. Sobolev spaces (Boston, MA: Academic Press, 1975).Google Scholar
4Ambrosio, L., Mortola, S. and Tortorelli, V. M.. Functionals with linear growth defined on vector valued BV functions. J. Math. Pures et Appt. 70 (1991), 269–323.Google Scholar
5Ambrosio, L., Fusco, N. and Pallara, D.. Functions of bounded variation and free discontinuity problems (Oxford: Oxford Science publications, Clarendon press, 2000).Google Scholar
6Babadjian, J. F.. Traces of functions of bounded deformation. Indiana Univ. Math. J. 64 (2015), 1271–1290.CrossRefGoogle Scholar
7Besov, O. V.. Integral estimates for differentiable functions on irregular domains. Doklady Mathematics 1 (2010), 87–90 (published in Doklady Academii Nauk, 430, 5 (2010) 583–585).CrossRefGoogle Scholar
8Bost, C., Cottet, G.-H. and Maitre, E.. Convergence analysis of a penalization method for the three-dimensional motion of a rigid body in an incompressible viscous fluid. SIAM J. Numer. Anal. 48 (2010), 131–1337.CrossRefGoogle Scholar
9Chemetov, N. V. and Nečasová, Š.. The motion of the rigid body in viscous fluid including collisions. Global solvability result. Nonlinear Anal.: Real World Appl. 34 (2017), 416–445.CrossRefGoogle Scholar
10Demengel, F. and Demengel, G.. Functional spaces for the theory of elliptic partial differential equations Translated from the 2007 French original by Reinie Erné. Universitext. (Springer, London; EDP Sciences, Les Ulis, 2012).CrossRefGoogle Scholar
11Evans, L. C. and Gariepy, R. E.. Measure theory and fine properties of functions (CRC Press, 1991).Google Scholar
12Federer, H.. Geometric measure theory (Springer, 1969).Google Scholar
13Feireisl, E., Hillairet, M. and Nečasová, Š.. On the motion of several rigid bodies in an incompressible non-Newtonian fluid. Nonlinearity 21 (2008), 1349–1366.CrossRefGoogle Scholar
14Gérard-Varet, D. and Hillairet, M.. Existence of weak solutions up to collision for viscous fluid-solid systems with slip. Comm. Pure Appl. Math. 67 (2014), 2022–2075.CrossRefGoogle Scholar
15Gérard-Varet, D., Hillairet, M. and Wang, C.. The influence of boundary conditions on the contact problem in a 3D Navier-Stokes flow. J. Math. Pures Appl. 103 (2015), 1–38.CrossRefGoogle Scholar
16Giusti, E.. Minimal surfaces and functions of bounded variation (Birkhttuser, 1984).CrossRefGoogle Scholar
17Grisvard, P.. Problemes aux limites dans des domaines avec points de rebroussement. Ann. Fac. Sci. Toulouse 4 (1995), 561–578.CrossRefGoogle Scholar
18Gunzburger, M. D., Lee, H.-C. and Seregin, G. A.. Global existence of weak solutions for viscous incompressible flows around a moving rigid body in three dimensions. J. Math. Fluid Mech. 2 (2000), 219–266.CrossRefGoogle Scholar
19Hesla, T. I.. Collision of smooth bodies in a viscous fluid: A mathematical investigation (2005), PhD Thesis – Minnesota.Google Scholar
20Hillairet, M.. Lack of collision between solid bodies in a 2D incompressible viscous flow. Comm. Partial Differ. Equ. 32 (2007), 1345–1371.CrossRefGoogle Scholar
21Hoffmann, K.-H. and Starovoitov, V. N.. On a motion of a solid body in a viscous fluid. Two dimensional case. Adv. Math. Sci. Appl. 9 (1999), 633–648.Google Scholar
22Judakov, N. V.. The solvability of the problem of the motion of a rigid body in a viscous incompressible fluid. (Russian) Dinamika Splošn. Sredy Vyp. 18 (1974), 249–253.Google Scholar
23Kilpelainen, T. and Maly, J.. Sobolev inequalities on sets with irregular boundaries. Z. Anal. Anwendungen 19 (2000), 369–380. The correction of the proof in ‘A correction to: Sobolev inequalities on sets with irregular boundaries’.CrossRefGoogle Scholar
24Labutin, D. A.. Definitiveness of Sobolev inequalities for a class of irregular domains. Proc. Steklov Inst. Math. 232 (2001), 211–215.Google Scholar
25Leoni, G.. A first course in Sobolev spaces. Graduate studies in mathematics, vol. 105 (Providence, Rhode Island: AMS, 2009).Google Scholar
26Maz'ya, V. G.. Classes of domains and embedding theorems for function spaces. Soviet Math. Dokl. 133 (1960), 882–885.Google Scholar
27Maz'ya, V. G. and Poborchi, S. V.. Differentiable functions on bad domains (River Edge, NJ: World Scientific Publishing Co., 1997).CrossRefGoogle Scholar
28Neustupa, J. and Penel, P.. Existence of a weak solution to the Navier-Stokes equation with Navier's boundary condition around striking bodies. Comptes Rendus Mathematique 347 (2009), 685–690.CrossRefGoogle Scholar
29Neustupa, J. and Penel, P.. A weak solvability of the Navier-Stokes equation with Navier's boundary condition around a ball striking the wall. In The book: advances in Mathematical Fluid Mechanics: dedicated to Giovanni Paolo Galdi, Rannacher, R., Sequeira, A. (eds) (Berlin: Springer-Verlag, 2010),pp. 385–408.CrossRefGoogle Scholar
30Planas, G. and Sueur, F.. On the ‘viscous incompressible fluid + rigid body’ system with Navier conditions. Annales de l'I.H.P. Analyse non linÃⒸaire 31 (2014), 55–80.Google Scholar
31San Martin, J. A., Starovoitov, V. and Tucsnak, M.. Global weak solutions for the two dimensional motion of several rigid bodies in an incompressible viscous fluid. Arch. Rational Mech. Anal. 161 (2002), 93–112.Google Scholar
32Starovoitov, V. N.. Behavior of a rigid body in an incompressible viscous fluid near boundary. In The book: International Series of Numerical Mathematics (Basel: Birkhäuser), vol. 147 (2003),pp. 313–327.Google Scholar
33Takahashi, T.. Analysis of strong solutions for the equations modeling the motion of a rigid-fluid system in a bounded domain. Advances in Differ. Equ. 8 (2003), 1499–1532.Google Scholar
34Temam, R.. Problèmes mathématique en plasticité' (Gauthier-Villars: Bordas, Paris, 1983).Google Scholar
35Temam, R. and Strang, G.. Functions of bounded deformation. Arch. Ration. Mech. Anal. 75 (1980), 7–21.CrossRefGoogle Scholar
36Vol'pert, A. I.. The spaces BV and quasilinear equations. Mat. Sb. 73 (1967), 255–302.Google Scholar
37Vol'pert, A. I. and Hudjaev, S. I.. Analysis in classes of discontinuous functions and equations of mathematical physics (Martinus Nijhoff Publishers, 1985).Google Scholar
38Weck, N.. Local compactness for linear elasticity in irregular domains. Math. Meth. Appl. Sci. 17 (1994), 107–113.CrossRefGoogle Scholar
39Ziemer, W.. Weakly differentiable functions (Springer, 1989).CrossRefGoogle Scholar