Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-01-13T17:24:09.315Z Has data issue: false hasContentIssue false
  • English
  • Français

Eine kritische Bemerkung zu Darstellungen der Schauderschen Beweistechnik für elliptische lineare Differentialgleichungen

Published online by Cambridge University Press:  14 November 2011

Manfred König
Manfred König
Affiliation:
Edelweiss Strasse 11, 8131 Berg-4-Höhenrain, Germany
Get access Rights & Permissions [Opens in a new window]

Synopsis

The object of this paper is to demonstrate, that with the open mapplng theorem of S.Banach one can prove very easily the following estimate

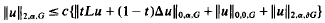
for all u ∈ C2,α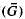 and 0 ≤ t ≤ 1, if one knows, that for all bounded G ⊂ Rn, with boundary ∂G ∈ C2,α and for all (f, g) ∈ C0,α 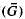× C2,α (∂G) Dirichle's problem Δu = f, u|∂G = g has a solution u ∈ C2,α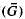. This estimate can be used to solve Dirichle's problem for a general linear elliptic equation by Schauder's method.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 80 , Issue 3-4 , 1978 , pp. 177 - 182
Copyright
Copyright © Royal Society of Edinburgh 1978

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Barrar, R. B.On Schauder's Paper on linear elliptic differential equations. J. Math. Anal. Appl. 3 (1961), 171–195.CrossRefGoogle Scholar
2Boboc, N. and Mustatǎ, P.Remarks on the existence of solutions of the Dirichlet problem for strongly elliptic linear operators of second order. Bull. Math. Soc. Sci. Math. R. S. Roumanie. 10 (1966), 75–85.Google Scholar
3Graves, L. M. The Estimates of Schauder and their Applications to Existence Theorems for Elliptic Differential Equations. Univ. Chicago, Invest. Theory Part. Diff. Eq. Techn. Report 1 (1956).Google Scholar
4Kellogg, O. D.On the derivatives of harmonic functions on the boundary. Trans. Amer. Math. Soc. 33 (1931), 486–510.CrossRefGoogle Scholar
5König, M.Über des Verhalten der Lösung des Dirichlet-problems am Rand des Gebietes, wenn der Rand zur Klasse C 2,α gehört. Proc. Roy. Soc. Edinburgh Sect. A, 80 (1978), 163–176.CrossRefGoogle Scholar
6Ladyzhenskaya, O. A. and Uralt'seva, N. N.Linear and Quasilinear Elliptic Equations (London: Academic Press, 1968).Google Scholar
7Schauder, J.Über lineare elliptische Differential-gleichunger zweiter Ordnung. Math. Z. 38 (1934), 257–282.CrossRefGoogle Scholar