Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-01-30T06:57:40.809Z Has data issue: false hasContentIssue false
  • English
  • Français

Delta-invariants of complete intersection log del Pezzo surfaces

Published online by Cambridge University Press:  10 May 2022

In-Kyun Kim  and
Joonyeong Won
In-Kyun Kim
Affiliation:
Department of Mathematics, Yonsei University, Seoul, Korea ([email protected])
Joonyeong Won
Affiliation:
Department of Mathematics, Ewha Womans University, Seoul, Korea ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that complete intersection log del Pezzo surfaces with amplitude one in weighted projective spaces are uniformly $K$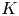-stable. As a result, they admit an orbifold Kähler–Einstein metric.

Keywords

K-stabilitydel Pezzo surfacecomplete intersectiondelta invariant
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 153 , Issue 3 , June 2023 , pp. 1021 - 1036
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Araujo, C.. Kähler-Einstein metrics for some quasi-smooth log del Pezzo surfaces. Trans. Amer. Math. Soc. 354 (2002), 4303–3312.CrossRefGoogle Scholar
Cheltsov, I., Park, J. and Shramov, C.. Exceptional del Pezzo hypersurfaces. J. Geom. Anal. 20 (2010), 787–816.CrossRefGoogle Scholar
Cheltsov, I., Park, J. and Shramov, C.. Delta invariants of singular del Pezzo surfaces, preprint arXiv:1809.09221 (2018).Google Scholar
Cheltsov, I., Rubinstein, Y. and Zhang, K.. Basis log canonical thresholds, local intersection estimates, and asymptotically log del Pezzo surfaces. Selecta Math. (N.S.) 25 (2019), 25–34.CrossRefGoogle Scholar
Cheltsov, I. and Zhang, K.. Delta invariants of smooth cubic surfaces. Eur. J. Math. 5 (2019), 729–762.CrossRefGoogle Scholar
Fujita, K.. On the uniform $K$-stability for some asymptotically log del Pezzo surfaces, preprint arXiv:1907.04998 (2019).Google Scholar
Fujita, K., Liu, Y., Süß, H., Zhang, K. and Zhuang, Z.. On the Cheltsov–Rubinstein conjecture, preprint arXiv:1907.02727 (2019).Google Scholar
Fujita, K. and Odaka, Y.. On the $K$-stability of Fano varieties and anticanonical divisors. Tohoku Math. J. (2) 70 (2018), 511–521.CrossRefGoogle Scholar
Johnson, J. and Kollár, J.. Kähler-Einstein metrics on log del Pezzo surfaces in weighted projective 3-spaces. Ann. de l'Institut Fourier 51 (2001), 69–79.CrossRefGoogle Scholar
Kim, I. and Park, J.. Log canonical thresholds of complete intersection log del Pezzo surfaces. Proc. Edinb. Math. Soc. (2) 58 (2015), 445–483.CrossRefGoogle Scholar
Kim, I. and Won, J.. Weakly exceptional singularities of log del Pezzo surfaces. Internat. J. Math. 30 (2019), 1950010.10.1142/S0129167X19500101CrossRefGoogle Scholar
Kollár, J.. Singularities of pairs. Proc. Symposia Pure Math. 62 (1997), 221–287.CrossRefGoogle Scholar
Li, C., Tian, G. and Wang, F.. On Yau–Tian–Donaldson conjecture for singular Fano varieties, preprint arXiv:1711.09530 (2017).Google Scholar
Park, J. and Won, J.. $K$-stability of smooth del Pezzo surfaces. Math. Ann. 372 (2018), 1239–1276.CrossRefGoogle Scholar
Park, J. and Won, J.. Simply connected Sasaki-Einstein rational homology 5-spheres, e-print arXiv:1905.13304 (2019).Google Scholar