Article contents
Degenerate Lyapunov functionals of a well-known prey–predator model with discrete delays
Published online by Cambridge University Press: 14 November 2011
Extract
It is commonly believed that, as far as stabilities are concerned, ‘small delays are negligible in some modelling processes’. However, to have an affirmative answerfor this common belief is still an open problem for many nonlinear equations. In this paper, the classical Lotka–Volterra prey–predator equation with discrete delays
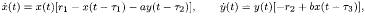
is considered, and, by using degenerate Lyapunov functionals method, an affirmative answer to this open problem on both local and global stabilities of the prey–predator delay equations is given. It is shown that degenerate Lyapunov functional method is a powerful tool for studying the stability of such nonlinear delay systems. A detailed and explicit procedure of constructing such functionals is provided. Furthermore, some explicit estimates on the allowable sizes of the delays are obtained.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 129 , Issue 4 , 1999 , pp. 755 - 771
- Copyright
- Copyright © Royal Society of Edinburgh 1999
References
- 3
- Cited by


