Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-01-25T20:40:42.355Z Has data issue: false hasContentIssue false
  • English
  • Français

Decay of weak solutions to Vlasov equation coupled with a shear thickening fluid

Part of: Foundations, constitutive equations, rheology Equations of mathematical physics and other areas of application Partial differential equations

Published online by Cambridge University Press:  02 December 2021

Jae-Myoung Kim
Jae-Myoung Kim*
Affiliation:
Department of Mathematics Education, Andong National University, Andong 36729, Republic of Korea ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that the energy norm of weak solutions to Vlasov equation coupled with a shear thickening fluid on the whole space has a decay rate the energy norm $E(t) \leq {C}/{(1+t)^{\alpha }}, \forall t \geq 0$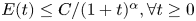 for $\alpha \in (0,3/2)$.

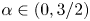Keywords

non-Newtonian fluidNavier–Stokes equationsVlasov equationdecay estimate

MSC classification

Primary: 35Q30: Navier-Stokes equations
Secondary: 76A05: Non-Newtonian fluids 35B35: Stability
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 153 , Issue 1 , February 2023 , pp. 167 - 176
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Astarita, G. and Marrucci, G.. Principles of non-Newtonian fluid mechanics (London, New York: McGraw-Hill, 1974).Google Scholar
Baranger, C. and Desvillettes, L.. Coupling Euler and Vlasov equation in the context of sprays: the local-in-time, classical solutions. J. Hyperbolic Differ. Equ. 3 (2006), 1–26.CrossRefGoogle Scholar
Boudin, L., Desvillettes, L., Grandmont, C. E. and Moussa, A.. Global existence of solution for the coupled Vlasov and Navier–Stokes equations. Differ. Int. Equ. 22 (2009), 1247–1271.Google Scholar
Goudon, T., Jabin, P.-E. and Vasseur, A.. Hydrodynamic limit for the Vlasov–Navier–Stokes equations I. Light particles regime. Indiana Univ. Math. J. 53 (2004), 1495–1515.CrossRefGoogle Scholar
Goudon, T., Jabin, P.-E. and Vasseur, A.. Hydrodynamic limit for the Vlasov–Navier–Stokes equations II. Fine particles regime. Indiana Univ. Math. J. 53 (2004), 1517–1536.CrossRefGoogle Scholar
Guo, B. and Zhu, P.. Algebraic $L^{2}$ decay for the solution to a class system of non-Newtonian fluid in ${{\mathbb {R}}}^{n}$. J. Math. Phys. 41 (2000), 349–356.CrossRefGoogle Scholar
Ha, S.-Y., Kim, H. K., Kim, J.-M., et al. On the global existence of weak solutions for the Cucker–Smale–Navier–Stokes system with shear thickening. Sci. China Math. 61 (2018), 2033–2052.CrossRefGoogle Scholar
Hamdache, K.. Global existence and large time behavior of solutions for the Vlasov–Stokes equations. Japan J. Indust. Appl. Math. 15 (1998), 51–74.CrossRefGoogle Scholar
Han-Kwan, D.. Large time behavior of small data solutions to the Vlasov–Navier–Stokes system on the whole space, arXiv:2006.09848.Google Scholar
Mucha, P., Peszek, J. and Pokorny, M.. Flocking particles in a non-Newtonian shear thickening fluid. Nonlinearity 31 (2018), 2703–2725.CrossRefGoogle Scholar
Nečasová, Š. and Penel, P.. $L^{2}$ decay for weak solution to equations of non-Newtionian incompressible fluids in the whole space. Nonlinear Anal. 47 (2001), 4181–4191.CrossRefGoogle Scholar
Wilkinson, W. L.. Non-Newtonian fluids: Fluid mechanics, mixing and heat transfer (London, New York: Pergamon Press, 1960).Google Scholar
Wiegner, M.. Decay results for weak solutions of the Navier–Stokes equations on $R^{n}$. J. London Math. Soc. (2) 35 (1987), 303–313.CrossRefGoogle Scholar