Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-01-14T13:52:50.156Z Has data issue: false hasContentIssue false
  • English
  • Français

Correspondences of completely regular semigroups and 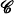-isomorphisms of semigroups

Published online by Cambridge University Press:  14 November 2011

Simon M. Goberstein
Simon M. Goberstein
Affiliation:
Department of Mathematics and Statistics, California State University, Chico, California 95929-0525, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Extract

A correspondence of a semigroup S is any subsemigroup of S × S, and the set of all correspondences of S, with the operations of composition and involution and the relation of set-theoretic inclusion, forms the bundle of correspondences of S, denoted by (S). For semigroups S and T, any isomorphism of (S) onto (T) is called a -isomorphism of S upon T. Similar notion can be introduced for other types of algebras and in the general frame of category theory. The principal goal of this paper is to study -isomorphisms of completely regular semigroups (that is, unions of groups) and of one other interesting class of semigroups.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 125 , Issue 3 , 1995 , pp. 625 - 637
Copyright
Copyright © Royal Society of Edinburgh 1995

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Baranskiǐ, V. A. and Trachtman, A. N.. Half-isomorphisms of rectangular bands of cancellative semigroups. Mat. Zap. Ural. Univ. 6 (1968), No. 3, 1–11 (in Russian).Google Scholar
2Bredihin, D. A.. Involuted semigroups of stable binary relations. In Studies in Algebra, No. 4, pp. 3–12 (Saratov, USSR: Saratov University Press, 1974 (in Russian)).Google Scholar
3Bredihin, D. A.. Bundles of correspondences of semigroups. In Contemporary Algebra, No. 4, pp. 31–47 (Leningrad, USSR: Leningrad Ped. Inst. Press, 1976 (in Russian)).Google Scholar
4Bredihin, D. A. RL-lattices of correspondences of groups. In Ordered Sets and Lattices, No. 5, pp. 7–11 (Saratov, USSR: Saratov University Press, 1978 (in Russian)).Google Scholar
5Bredihin, D. A.. Bundles of correspondences and ℛ-isomorphisms of congruence-permutable algebras. In Theory of Semigroups and Its Applications, pp. 4–9 (Saratov, USSR: Saratov University Press, 1984 (in Russian)).Google Scholar
6Burgin, M. S.. Categories with involution and correspondences in γ-categories. Trans. Moscow Math. Soc. 22 (English transl.) (1970), 181–257.Google Scholar
7Calenko, M. Š.. Classification of correspondence categories and types of regularity for categories. Trans. Moscow Math. Soc. (English transl.) (1982) Issue 1, 239–82.Google Scholar
8Clifford, A. H. and Preston, G. B.. The Algebraic Theory of Semigroups, Vol. I, Mathematical Surveys 7 (Providence, R.I.: American Mathematical Society, 1961).Google Scholar
9Easdown, D.. Biordered sets come from semigroups. J. Algebra 96 (1985), 581–91.CrossRefGoogle Scholar
10Gel'fand, I. M. and Ponomarev, V. A.. Indecomposable representations of the Lorentz group. Russian Math. Surveys 23 (English transl.) (1968), No. 2, 1–58.CrossRefGoogle Scholar
11Goberstein, S. M.. Correspondences of semigroups. In Semigroups: Theory and Applications, Lecture Notes in Mathematics 1320, pp. 141–9 (Berlin: Springer, 1988).CrossRefGoogle Scholar
12Goberstein, S. M.. Inverse semigroups determined by their bundles of correspondences. J. Algebra 125 (1989), 474–88.CrossRefGoogle Scholar
13Goberstein, S. M.. Bundles of correspondences of orthodox semigroups. In Monash Conference on Semigroup Theory in Honour of G. B. Preston, eds Hall, T. E., Jones, P. R. and Meakin, J. C., pp. 77–85 (Singapore: World Scientific, 1991).Google Scholar
14Goberstein, S. M.. On orthodox semigroups determined by their bundles of correspondences. Pacific J. Math. 153 (1992), 71–84.CrossRefGoogle Scholar
15Howie, J. M.. An Introduction to Semigroup Theory (London: Academic Press, 1976).Google Scholar
16Iskander, A. A.. The lattice of correspondences of a universal algebra. Izv. Akad. Nauk SSSR, Ser. Mat. 29 (1965), 1357–72 (in Russian).Google Scholar
17Jones, P. R.. Basis properties for inverse semigroups. J. Algebra 50 (1978), 135–52.CrossRefGoogle Scholar
18Kurosh, A. G.. The Theory of Groups, 3rd edn (Moscow: Nauka, 1967 (in Russian)).Google Scholar
19Kurosh, A. G.. General Algebra, Lectures in the 1969/1970 Academic Year (Moscow: Nauka, 1974 (in Russian)).Google Scholar
20Lane, S. Mac. An algebra of additive relations. Proc. Nat. Acad. Sci. U.S.A. 47 (1961), 1043–51.CrossRefGoogle Scholar
21Lane, S. Mac. Homology (Berlin: Springer, 1963).CrossRefGoogle Scholar
22Nambooripad, K. S. S.. Structure of regular semigroups. I. Mem. Amer. Math. Soc. 22 (1979), No. 224.Google Scholar
23Puppe, D.. Korrespondenzen in Abelschen Kategorien. Math. Ann. 148 (1962), 1–30.CrossRefGoogle Scholar
24Rottländer, A.. Nachweis der Existenz nicht-isomorpher Gruppen von gleicher Situation der Untergruppen. Math. Z. 28 (1928), 641–53.CrossRefGoogle Scholar
25Schein, B. M.. An idempotent semigroup is determined by the pseudogroup of its local automorphisms. Mat. Zap. Ural Univ. 7 (1970), No. 3, 222–33 (in Russian).Google Scholar
26Scott, W. R.. Half-homomorphisms of groups. Proc. Amer. Math. Soc. 8 (1957). 1141–4.CrossRefGoogle Scholar
27Shevrin, L. N.. Half-isomorphisms of cancellative semigroups. Izv. Akad. Nauk SSSR, Ser. Mat. 31 (1967), 957–64 (in Russian).Google Scholar
28Suzuki, M.. Structure of a Group and the Structure of Its Lattice of Subgroups (Berlin: Springer, 1956).CrossRefGoogle Scholar
29Žitomirskiǐ, G. I.. Stable binary relations on universal algebras. Mat. Sb. 82 (1970), 163–74 (in Russian).Google Scholar