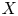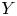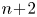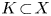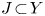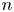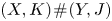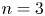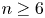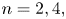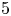1. Introduction
In the smooth category, the fact that the connected sum of manifolds is well-defined depends on a result first proved by Cerf [Reference Cerf7] and Palais [Reference Palais18]. In the topological category the result is much deeper. For $n \ge 6$![]() , the theorem that the connected sum of topological $n$
, the theorem that the connected sum of topological $n$![]() –manifolds is well-defined is a consequence of the Annulus Conjecture, proved by Kirby [Reference Kirby14]. In dimensions $n=4$
–manifolds is well-defined is a consequence of the Annulus Conjecture, proved by Kirby [Reference Kirby14]. In dimensions $n=4$![]() and $n=5$
and $n=5$![]() the proof relies on Freedman and Quinn's work concerning topological 4–manifolds [Reference Freedman10, Reference Freedman and Quinn11].
the proof relies on Freedman and Quinn's work concerning topological 4–manifolds [Reference Freedman10, Reference Freedman and Quinn11].
For smooth manifolds, proving that the connected sum of submanifolds is well-defined is also a consequence of the result proved by Palais and by Cerf; a summary is presented in an appendix to this paper. Proving that connected sums of locally flat $n$![]() –dimensional submanifolds of topological manifolds of dimension $n + 2$
–dimensional submanifolds of topological manifolds of dimension $n + 2$![]() is well-defined is more challenging: the proof presented here relies on the existence and uniqueness of normal bundles in codimension two, results that call on the $s$
is well-defined is more challenging: the proof presented here relies on the existence and uniqueness of normal bundles in codimension two, results that call on the $s$![]() –cobordism theorem with fundamental group ${\mathbb {Z}}$
–cobordism theorem with fundamental group ${\mathbb {Z}}$![]() , proved by Kirby-Siebenmann [Reference Kirby and Siebenmann16, § III, 3.4] for higher dimensions and appearing in [Reference Freedman and Quinn11, theorem 7.1A] for cobordisms of dimension five.
, proved by Kirby-Siebenmann [Reference Kirby and Siebenmann16, § III, 3.4] for higher dimensions and appearing in [Reference Freedman and Quinn11, theorem 7.1A] for cobordisms of dimension five.
Cappell and Shaneson [Reference Cappell and Shaneson6, proposition, Page 34] briefly sketched a proof of the key result that is needed in showing that connected sums are well-defined for $n\!\ge \!3$![]() in the special case of knotted spheres in $S^n$
in the special case of knotted spheres in $S^n$![]() . The proof here roughly follows their approach, but it addresses some issues that were not considered in [Reference Cappell and Shaneson6]. In particular, the cases of $n = 2, n=4$
. The proof here roughly follows their approach, but it addresses some issues that were not considered in [Reference Cappell and Shaneson6]. In particular, the cases of $n = 2, n=4$![]() and $n=5$
and $n=5$![]() require the use of results of Freedman-Quinn. In addition, at the time [Reference Cappell and Shaneson6] was written, details of the necessary topological manifold theory had not been published.
require the use of results of Freedman-Quinn. In addition, at the time [Reference Cappell and Shaneson6] was written, details of the necessary topological manifold theory had not been published.
Conventions. Manifolds of dimension $n$![]() are second countable Hausdorff spaces with the property that every point has a neighbourhood homeomorphic to ${\mathbb {R}}^n$
are second countable Hausdorff spaces with the property that every point has a neighbourhood homeomorphic to ${\mathbb {R}}^n$![]() . A $k$
. A $k$![]() –submanifold $N$
–submanifold $N$![]() of an $n$
of an $n$![]() –manifold $M$
–manifold $M$![]() is a pair $(M,N)$
is a pair $(M,N)$![]() of manifolds, $N \subset M$
of manifolds, $N \subset M$![]() , that is locally modelled on $({\mathbb {R}}^{k} \times {\mathbb {R}}^{n-k} , {\mathbb {R}}^{k} \times \{0\})$
, that is locally modelled on $({\mathbb {R}}^{k} \times {\mathbb {R}}^{n-k} , {\mathbb {R}}^{k} \times \{0\})$![]() . We will refer to these as locally-flat submanifolds to emphasize the structure. We will work exclusively with manifolds that are oriented. As will be made precise in § 3, we will show that if $F_1$
. We will refer to these as locally-flat submanifolds to emphasize the structure. We will work exclusively with manifolds that are oriented. As will be made precise in § 3, we will show that if $F_1$![]() and $F_2$
and $F_2$![]() are connected, $n$
are connected, $n$![]() –dimensional submanifolds of $(n + 2)$
–dimensional submanifolds of $(n + 2)$![]() –manifolds $W_1$
–manifolds $W_1$![]() and $W_2$
and $W_2$![]() , then $(W_1, F_1)\! \mathbin {\#}\! (W_2,F_2)$
, then $(W_1, F_1)\! \mathbin {\#}\! (W_2,F_2)$![]() is a well-defined homeomorphism class of topological pairs.
is a well-defined homeomorphism class of topological pairs.
The results here extend to the case of interior connected sums of manifold pairs with boundary. We do not consider the case of boundary connected sums of manifold pairs.
References. The key background material for our work is in the books by Kirby-Siebenmann [Reference Kirby and Siebenmann16] and by Freedman-Quinn [Reference Freedman and Quinn11]. An early version of the current paper that included an appendix with an overview of that material is available at [Reference Livingston17]. The book [1] provides a detailed exposition of the foundations of topological four-manifold theory.
2. Connected sums of manifolds
Initially we want to work with manifolds, not with homeomorphism classes of manifolds. Constructions of spaces, such as connected sums, are built from quotient spaces and these are typically not well-defined spaces, but rather are defined up to homeomorphism. To remedy this, we will assume that one has chosen a convention so that the disjoint union of spaces is a well-defined space. With this, adjunction spaces are well-defined as spaces.
Let $n >0$![]() and let $W_1$
and let $W_1$![]() and $W_2$
and $W_2$![]() be oriented connected $(n+2)$
be oriented connected $(n+2)$![]() –manifolds. Choose embeddings $\phi \colon \! {\mathbb {R}}^{n+2} \to W_1$
–manifolds. Choose embeddings $\phi \colon \! {\mathbb {R}}^{n+2} \to W_1$![]() and $\psi \colon \! {\mathbb {R}}^{n+2} \to W_2$
and $\psi \colon \! {\mathbb {R}}^{n+2} \to W_2$![]() , where $\phi$
, where $\phi$![]() is orientation preserving and $\psi$
is orientation preserving and $\psi$![]() is orientation reversing. The connected sum of manifolds is defined as
is orientation reversing. The connected sum of manifolds is defined as
The equivalence relation identifies $\phi (\theta )$![]() with $\psi (\theta )$
with $\psi (\theta )$![]() for $\theta \in S^{n+1}$
for $\theta \in S^{n+1}$![]() . There is a canonical embedding $\phi '\colon \! S^{n+1}\to W_1 \mathbin {\#}_{\phi, \psi } W_2$
. There is a canonical embedding $\phi '\colon \! S^{n+1}\to W_1 \mathbin {\#}_{\phi, \psi } W_2$![]() , yielding a pair that we denote $(W_1 \mathbin {\#}_{\phi, \psi } W_2, \phi '(S^{n+1}))$
, yielding a pair that we denote $(W_1 \mathbin {\#}_{\phi, \psi } W_2, \phi '(S^{n+1}))$![]() . We leave the following result to the reader.
. We leave the following result to the reader.
Theorem 2.1 The space $W_1 \mathbin {\#}_{\phi, \psi } W_2$![]() is an oriented topological manifold. The natural inclusions of $W_1 {\setminus} \text {Int}(\phi (B^{n+2}))$
is an oriented topological manifold. The natural inclusions of $W_1 {\setminus} \text {Int}(\phi (B^{n+2}))$![]() and $W_2 {\setminus} \text {Int}(\psi (B^{n+2}))$
and $W_2 {\setminus} \text {Int}(\psi (B^{n+2}))$![]() into $W_1 \mathbin {\#}_{\phi, \psi } W_2$
into $W_1 \mathbin {\#}_{\phi, \psi } W_2$![]() are orientation preserving embeddings. The pair $(W_1 \mathbin {\#}_{\phi, \psi } W_2 , \phi '(S^{n+1}))$
are orientation preserving embeddings. The pair $(W_1 \mathbin {\#}_{\phi, \psi } W_2 , \phi '(S^{n+1}))$![]() is locally flat.
is locally flat.
The following result implies that the connected sum of connected oriented topological manifolds $W_1$![]() and $W_2$
and $W_2$![]() is a well-defined homeomorphism class, usually denoted $W_1 \mathbin {\#} W_2$
is a well-defined homeomorphism class, usually denoted $W_1 \mathbin {\#} W_2$![]() . Notice that in the following theorem, we are working with manifolds, not homeomorphism classes.
. Notice that in the following theorem, we are working with manifolds, not homeomorphism classes.
Theorem 2.2 Given embeddings $\phi _1$![]() , $\phi _2$
, $\phi _2$![]() , $\psi _1$
, $\psi _1$![]() and $\psi _2$
and $\psi _2$![]() as above, there exists an orientation preserving homeomorphism $(W_1 \mathbin {\#}_{\phi _1, \psi _1} W_2 , \phi _1'(S^{n+1})) \to (W_1 \mathbin {\#}_{\phi _2, \psi _2} W_2 , \phi _2'(S^{n+1}))$
as above, there exists an orientation preserving homeomorphism $(W_1 \mathbin {\#}_{\phi _1, \psi _1} W_2 , \phi _1'(S^{n+1})) \to (W_1 \mathbin {\#}_{\phi _2, \psi _2} W_2 , \phi _2'(S^{n+1}))$![]() .
.
Proof. We focus on $\phi _1$![]() and $\phi _2$
and $\phi _2$![]() . Here is a summary of the key steps.
. Here is a summary of the key steps.
(1) There exists a homeomorphism $F\colon \! W_1 \to W_1$
 for which $F(\phi _2(0)) = \phi _1(0)$
for which $F(\phi _2(0)) = \phi _1(0)$ . Using this, we can assume that $\phi _2(0) = \phi _1(0)$
. Using this, we can assume that $\phi _2(0) = \phi _1(0)$ .
.(2) By composing with another homeomorphism of $W_1$
 , we can also arrange that $\phi _2(B^{n+2} )\subset \text {Int}(\phi _1(B^{n+2}))$
, we can also arrange that $\phi _2(B^{n+2} )\subset \text {Int}(\phi _1(B^{n+2}))$ .
.(3) The Annulus Conjecture permits us to arrange that $\phi _2(B^{n+2}) = \phi _1(B^{n+2})$
 . (The Annulus Conjecture was proved by Kirby [Reference Kirby14] for $n+2 \ge 5$
. (The Annulus Conjecture was proved by Kirby [Reference Kirby14] for $n+2 \ge 5$ ; in dimension four it was proved by Quinn [Reference Quinn19, § 2.2]. See Edwards [Reference Edwards9] for a survey.)
; in dimension four it was proved by Quinn [Reference Quinn19, § 2.2]. See Edwards [Reference Edwards9] for a survey.)(4) We need to arrange that $\phi _1$
 and $\phi _2$
and $\phi _2$ agree on $S^{n+1}$
agree on $S^{n+1}$ . Consider $F\colon \! S^{n+1} \to S^{n+1}$
. Consider $F\colon \! S^{n+1} \to S^{n+1}$ defined by $\phi _2^{-1} \circ \phi _1$
defined by $\phi _2^{-1} \circ \phi _1$ . The truth of the Stable Homeomorphism Conjecture implies that $F$
. The truth of the Stable Homeomorphism Conjecture implies that $F$ is a composition of maps, each of which is the identity on some non-empty open set. (For $n\ge 5$
is a composition of maps, each of which is the identity on some non-empty open set. (For $n\ge 5$ , the Stable Homeomorphism Conjecture was proved by Kirby [Reference Kirby14]. Quinn's proof of the Annulus Conjecture for $n = 4$
, the Stable Homeomorphism Conjecture was proved by Kirby [Reference Kirby14]. Quinn's proof of the Annulus Conjecture for $n = 4$ yields a proof of the Stable Homeomorphism Conjecture in that dimension. The relationships between the Annulus Conjecture and the Stable Homeomorphism Conjecture was first identified by Brown and Gluck in a series of papers [Reference Brown and Gluck3–Reference Brown and Gluck5]. In particular, see [Reference Brown and Gluck3, § 9].)
yields a proof of the Stable Homeomorphism Conjecture in that dimension. The relationships between the Annulus Conjecture and the Stable Homeomorphism Conjecture was first identified by Brown and Gluck in a series of papers [Reference Brown and Gluck3–Reference Brown and Gluck5]. In particular, see [Reference Brown and Gluck3, § 9].)Assuming that $F$
 is the identity on a closed ball $B$
is the identity on a closed ball $B$ in $S^{n+1}$
in $S^{n+1}$ , we can use the Alexander Trick [Reference Alexander2] applied to the closure of the complement of $B$
, we can use the Alexander Trick [Reference Alexander2] applied to the closure of the complement of $B$ to find an isotopy from $F$
to find an isotopy from $F$ to the identity map.
to the identity map.(5) A tubular neighbourhood of $\phi _1(S^{n+1})$
 can be used to extend the isotopy constructed in the previous step to build an isotopy of $W_1$
can be used to extend the isotopy constructed in the previous step to build an isotopy of $W_1$ that carries $\phi _2$
that carries $\phi _2$ to a new embedding that agrees with $\phi _1$
to a new embedding that agrees with $\phi _1$ on $S^{n+1}$
on $S^{n+1}$ , as needed to complete the proof.
, as needed to complete the proof.
3. Connected sums of pairs
Let $n >0$![]() and suppose that $F_1$
and suppose that $F_1$![]() and $F_2$
and $F_2$![]() are $n$
are $n$![]() –dimensional oriented, locally flat, connected submanifolds of $(n\!+\!2)$
–dimensional oriented, locally flat, connected submanifolds of $(n\!+\!2)$![]() –dimensional oriented manifolds $W_1$
–dimensional oriented manifolds $W_1$![]() and $W_2$
and $W_2$![]() . Local flatness ensures that we can choose an orientation preserving embedding $\phi \colon \! {\mathbb {R}}^{n+2} \to W_1$
. Local flatness ensures that we can choose an orientation preserving embedding $\phi \colon \! {\mathbb {R}}^{n+2} \to W_1$![]() such that $\phi ^{-1}(F_1) = {\mathbb {R}}^n\times \{0\}$
such that $\phi ^{-1}(F_1) = {\mathbb {R}}^n\times \{0\}$![]() . We view such an embedding as a map of pairs: $\phi \colon \! ({\mathbb {R}}^{n+2}, {\mathbb {R}}^n) \to (W_1, F_1)$
. We view such an embedding as a map of pairs: $\phi \colon \! ({\mathbb {R}}^{n+2}, {\mathbb {R}}^n) \to (W_1, F_1)$![]() . Similarly, choose an orientation reversing embedding $\psi \colon \! ({\mathbb {R}}^{n+2}, {\mathbb {R}}^n) \to (W_2, F_2)$
. Similarly, choose an orientation reversing embedding $\psi \colon \! ({\mathbb {R}}^{n+2}, {\mathbb {R}}^n) \to (W_2, F_2)$![]() . We have the unit balls $B^{n+2} \subset {\mathbb {R}}^{n+2}$
. We have the unit balls $B^{n+2} \subset {\mathbb {R}}^{n+2}$![]() and $B^{n}\subset {\mathbb {R}}^n \subset {\mathbb {R}}^{n+2}$
and $B^{n}\subset {\mathbb {R}}^n \subset {\mathbb {R}}^{n+2}$![]() .
.
The connected sum of pairs $(W_1, F_1)\mathbin {\#}_{\phi, \psi } (W_2, F_2 )$![]() is defined as follows.
is defined as follows.

The equivalence relation identifies $\phi (\theta )$![]() with $\psi (\theta )$
with $\psi (\theta )$![]() for $\theta \in S^{n+1}$
for $\theta \in S^{n+1}$![]() . The following result is straighforward.
. The following result is straighforward.
Theorem 3.1 Let $\overline {\phi }$![]() and $\overline {\psi }$
and $\overline {\psi }$![]() be the restrictions of $\phi$
be the restrictions of $\phi$![]() and $\psi$
and $\psi$![]() to $R^{n}$
to $R^{n}$![]() . There is a natural inclusion $F_1 \mathbin {\#}_{\overline {\phi }, \overline {\psi }} F_2 \subset W_1 \mathbin {\#}_{\phi, \psi } W_2$
. There is a natural inclusion $F_1 \mathbin {\#}_{\overline {\phi }, \overline {\psi }} F_2 \subset W_1 \mathbin {\#}_{\phi, \psi } W_2$![]() as a locally flat submanifold. Via this inclusion there is a homeomorphism
as a locally flat submanifold. Via this inclusion there is a homeomorphism
Our main result is the following.
Theorem 3.2 Given pairs of embeddings, $(\phi _1, \psi _1)$![]() and $(\phi _2, \psi _2)$
and $(\phi _2, \psi _2)$![]() , the manifold pairs $(W_1, F_1)\mathbin {\#}_{\phi _1, \psi _1} (W_2, F_2 )$
, the manifold pairs $(W_1, F_1)\mathbin {\#}_{\phi _1, \psi _1} (W_2, F_2 )$![]() and $(W_1, F_1)\mathbin {\#}_{\phi _2, \psi _2} (W_2, F_2)$
and $(W_1, F_1)\mathbin {\#}_{\phi _2, \psi _2} (W_2, F_2)$![]() are oriented homeomorphic. A homeomorphism can be chosen so that it restricts to be a homeomorphism of the splitting $(n\!+\!1)$
are oriented homeomorphic. A homeomorphism can be chosen so that it restricts to be a homeomorphism of the splitting $(n\!+\!1)$![]() –spheres.
–spheres.
The proof follows readily from three lemmas. The first is elementary. The second is the deepest, depending on the existence and uniqueness theorems for normal bundles of codimension two submanifolds. The third, though slightly technical, is elementary. In the second two, we change our perspective, viewing $({\mathbb {R}}^{n+2}, {\mathbb {R}}^n)$![]() as the pair $({\mathbb {R}}^n \times {\mathbb {R}}^2, {\mathbb {R}}^n \times \{0\})$
as the pair $({\mathbb {R}}^n \times {\mathbb {R}}^2, {\mathbb {R}}^n \times \{0\})$![]() .
.
Lemma 3.3 Let $F \subset W$![]() be a connected, codimension-two, locally flat submanifold and let $\phi \colon \! ({\mathbb {R}}^{n+2}, {\mathbb {R}}^n) \to (W, F)$
be a connected, codimension-two, locally flat submanifold and let $\phi \colon \! ({\mathbb {R}}^{n+2}, {\mathbb {R}}^n) \to (W, F)$![]() and $\phi ' \colon \! ({\mathbb {R}}^{n+2}, {\mathbb {R}}^n) \to (W, F)$
and $\phi ' \colon \! ({\mathbb {R}}^{n+2}, {\mathbb {R}}^n) \to (W, F)$![]() be embeddings. Then there is an orientation preserving self-homeomorphism of $(W,F)$
be embeddings. Then there is an orientation preserving self-homeomorphism of $(W,F)$![]() that carries $\phi '$
that carries $\phi '$![]() to an embedding $\phi '' \colon \! ({\mathbb {R}}^{n+2}, {\mathbb {R}}^n) \to (W, F)$
to an embedding $\phi '' \colon \! ({\mathbb {R}}^{n+2}, {\mathbb {R}}^n) \to (W, F)$![]() for which $\phi '' ( (B^{n+2}, B^n) )\subset \text {Int} (\phi ( (B^{n+2}, B^n)))$
for which $\phi '' ( (B^{n+2}, B^n) )\subset \text {Int} (\phi ( (B^{n+2}, B^n)))$![]() .
.
Proof. The proof follows readily from the next two observations.
(1) Let $a$
 and $b$
and $b$ be points on $F$
be points on $F$ . Then there is an orientation preserving homeomorphism $h\colon \! (W,F) \to (W,F)$
. Then there is an orientation preserving homeomorphism $h\colon \! (W,F) \to (W,F)$ for which $h(a) = b$
for which $h(a) = b$ . To prove this, consider the set
\[ B = \{ x \in F \ \big| \ \text{there exists an } h \colon\! (W,F) \to (W,F) \text{ for which } h(a) = x \}. \]Working locally, one can prove that $B$
. To prove this, consider the set
\[ B = \{ x \in F \ \big| \ \text{there exists an } h \colon\! (W,F) \to (W,F) \text{ for which } h(a) = x \}. \]Working locally, one can prove that $B$
 is both open and closed.
is both open and closed.(2) To ensure that $\phi '' ( (B^{n+2}, B^n) )\subset \text {Int}(\phi ( (B^{n+2}, B^n)))$
 we can again work locally, using the following observation. Let $U$
we can again work locally, using the following observation. Let $U$ be an arbitrary neighbourhood of $0 \in {\mathbb {R}}^{n+2}$
be an arbitrary neighbourhood of $0 \in {\mathbb {R}}^{n+2}$ . Then there is a homeomorphism $h \colon \! ({\mathbb {R}}^{n+2} , {\mathbb {R}}^n ) \to ({\mathbb {R}}^{n+2} , {\mathbb {R}}^n)$
. Then there is a homeomorphism $h \colon \! ({\mathbb {R}}^{n+2} , {\mathbb {R}}^n ) \to ({\mathbb {R}}^{n+2} , {\mathbb {R}}^n)$ for which $h(B^{n+2}) \subset U$
for which $h(B^{n+2}) \subset U$ and for which $h(x) = x$
and for which $h(x) = x$ for all $x$
for all $x$ with $\|x\| \ge 2$
with $\|x\| \ge 2$ .
.
Lemma 3.4 Let $\phi \colon \! (B^n \times B^2, B^n \times \{0\}) \to \text {Int} \, ((B^n \times B^2, B^n \times \{0\}) )$![]() be an embedding satisfying $\phi ^{-1}(B^n \times \{0\}) = B^n \times \{0\}$
be an embedding satisfying $\phi ^{-1}(B^n \times \{0\}) = B^n \times \{0\}$![]() . Assume that $\phi$
. Assume that $\phi$![]() extends to an embedding of an open neighbourhood of $B^n \times B^2 \subset {\mathbb {R}}^{n+2}$
extends to an embedding of an open neighbourhood of $B^n \times B^2 \subset {\mathbb {R}}^{n+2}$![]() . Then there is an ambient isotopy of $({\mathbb {R}}^n \times {\mathbb {R}}^2, {\mathbb {R}}^n \times \{0\})$
. Then there is an ambient isotopy of $({\mathbb {R}}^n \times {\mathbb {R}}^2, {\mathbb {R}}^n \times \{0\})$![]() carrying $\phi$
carrying $\phi$![]() to an embedding $\phi '$
to an embedding $\phi '$![]() such that $\phi ' ( (B^n \times B^2, B^n \times \{0\}) ) = (B^n \times B^2, B^n \times \{0\})$
such that $\phi ' ( (B^n \times B^2, B^n \times \{0\}) ) = (B^n \times B^2, B^n \times \{0\})$![]() . Furthermore, the isotopy can be chosen so that $\phi '$
. Furthermore, the isotopy can be chosen so that $\phi '$![]() is of the form $\phi '(x,y) = (\phi _1(x), \phi _2(x,y))$
is of the form $\phi '(x,y) = (\phi _1(x), \phi _2(x,y))$![]() .
.
Proof. The Annulus Conjecture in dimension $n$![]() implies that the image $\phi (B^n \times \{0\}) \subset \text {Int}(B^n \times \{0\})$
implies that the image $\phi (B^n \times \{0\}) \subset \text {Int}(B^n \times \{0\})$![]() is isotopic (in ${\mathbb {R}}^{n} \times \{0\}$
is isotopic (in ${\mathbb {R}}^{n} \times \{0\}$![]() ) to $B^n \times \{0\}$
) to $B^n \times \{0\}$![]() . We can extend this to an isotopy of ${\mathbb {R}}^n \times \{0\}$
. We can extend this to an isotopy of ${\mathbb {R}}^n \times \{0\}$![]() and then use the product structure to extend this isotopy to ${\mathbb {R}}^{n+2}$
and then use the product structure to extend this isotopy to ${\mathbb {R}}^{n+2}$![]() . With this, we can assume that $\phi (B^n \times \{0\}) = B^n \times \{0\}$
. With this, we can assume that $\phi (B^n \times \{0\}) = B^n \times \{0\}$![]() . Notice that after the isotopy, it is not necessarily the case that $\phi (B^n \times B^2) \subset B^n \times B^2$
. Notice that after the isotopy, it is not necessarily the case that $\phi (B^n \times B^2) \subset B^n \times B^2$![]() .
.
The condition that $\phi$![]() has an extension to a neighbourhood in ${\mathbb {R}}^{n+2}$
has an extension to a neighbourhood in ${\mathbb {R}}^{n+2}$![]() then ensures that the image $\phi (B^n \times B^2)$
then ensures that the image $\phi (B^n \times B^2)$![]() forms a normal bundle over $B^n \times \{0\}$
forms a normal bundle over $B^n \times \{0\}$![]() , which, by the extension theorem for bundles, is a sub-bundle of a normal bundle to ${\mathbb {R}}^n \times \{0\}$
, which, by the extension theorem for bundles, is a sub-bundle of a normal bundle to ${\mathbb {R}}^n \times \{0\}$![]() in ${\mathbb {R}}^{n+2}$
in ${\mathbb {R}}^{n+2}$![]() . By the uniqueness theorem for normal bundles, there is a fibre preserving ambient isotopy carrying one bundle to the other. Restricting to the image of $\phi$
. By the uniqueness theorem for normal bundles, there is a fibre preserving ambient isotopy carrying one bundle to the other. Restricting to the image of $\phi$![]() gives the desired result.
gives the desired result.
The existence and uniqueness results for normal bundles that we used above appear in Kirby-Siebenmann [Reference Kirby and Siebenmann15] for the higher dimensional case and in Freedman-Quinn [Reference Freedman and Quinn11, § 9.3] for dimension 4. The necessary isotopy extension result was proved by Edwards-Kirby [Reference Edwards and Kirby8, corollaries 1.3 and 1.4].
We now assume that $\phi \colon \! (B^n \times B^2, B^n \times \{0\}) \to (B^n \times B^2, B^n \times \{0\})$![]() is an orientation preserving homeomorphism of pairs that preserves the product structure in the sense that $\phi$
is an orientation preserving homeomorphism of pairs that preserves the product structure in the sense that $\phi$![]() can be decomposed as $\phi (x,y) = (\phi _1(x), \phi _2(x,y))$
can be decomposed as $\phi (x,y) = (\phi _1(x), \phi _2(x,y))$![]() for functions $\phi _1$
for functions $\phi _1$![]() and $\phi _2$
and $\phi _2$![]() .
.
Lemma 3.5 The map $\phi$![]() is isotopic to the identity as a map of pairs.
is isotopic to the identity as a map of pairs.
Proof. Consider $\phi _1 = \phi \big |_{B^n}$![]() . This is an orientation preserving homeomorphism of $B^n$
. This is an orientation preserving homeomorphism of $B^n$![]() . As described in the proof of theorem 2.2, the restriction to the boundary $S^{n-1}$
. As described in the proof of theorem 2.2, the restriction to the boundary $S^{n-1}$![]() is isotopic to the identity. By the Alexander trick, this isotopy extends to $B^n$
is isotopic to the identity. By the Alexander trick, this isotopy extends to $B^n$![]() . The product structure permits us to extend this isotopy to $B^n \times B^2$
. The product structure permits us to extend this isotopy to $B^n \times B^2$![]() , and thus we can assume that $\phi _1$
, and thus we can assume that $\phi _1$![]() is the identity and $\phi$
is the identity and $\phi$![]() is of the form
is of the form
The function $\phi _2$![]() defines a map from $B^n$
defines a map from $B^n$![]() to the orientation preserving homeomorphism group of the 2–ball fixing the origin, $\psi \colon \! B^n \to \text {Homeo}_+(B^2, 0)$
to the orientation preserving homeomorphism group of the 2–ball fixing the origin, $\psi \colon \! B^n \to \text {Homeo}_+(B^2, 0)$![]() ; that is, $\psi (x)(y) = \phi _2(x,y)$
; that is, $\psi (x)(y) = \phi _2(x,y)$![]() .
.
A coning construction defines an injection
The Alexander trick provides a deformation retraction from $\text {Homeo}_+(B^2)$![]() to the image of $\text {Homeo}_+(S^1)$
to the image of $\text {Homeo}_+(S^1)$![]() , and a check of its proof shows that the deformation preserves $\text {Homeo}_+(B^2, 0)$
, and a check of its proof shows that the deformation preserves $\text {Homeo}_+(B^2, 0)$![]() . The space $\text {Homeo}_+(S^1)$
. The space $\text {Homeo}_+(S^1)$![]() deformation retracts to $SO(2)$
deformation retracts to $SO(2)$![]() (see [Reference Ghys12, 4.2] for a proof) and so $\text {Homeo}_+(B^2, 0)$
(see [Reference Ghys12, 4.2] for a proof) and so $\text {Homeo}_+(B^2, 0)$![]() is path connected. Thus $\psi$
is path connected. Thus $\psi$![]() is homotopic to the constant map for which $\psi (x)$
is homotopic to the constant map for which $\psi (x)$![]() is the identity for all $x$
is the identity for all $x$![]() . This homotopy provides the desired isotopy of $\phi$
. This homotopy provides the desired isotopy of $\phi$![]() , completing the proof.
, completing the proof.
4. Problems
Problem 4.1 For $i =1$![]() and $2$
and $2$![]() , let $F_i^n \subset W_i^{n+k}$
, let $F_i^n \subset W_i^{n+k}$![]() be connected oriented locally flat codimension $k$
be connected oriented locally flat codimension $k$![]() submanifolds of oriented topological manifolds. Prove that the connect sum $(W_1, F_1) \mathbin {\#} (W_2, F_2)$
submanifolds of oriented topological manifolds. Prove that the connect sum $(W_1, F_1) \mathbin {\#} (W_2, F_2)$![]() is well-defined up to homeomorphism. More precisely, prove the higher codimension analogue of theorem 2.2.
is well-defined up to homeomorphism. More precisely, prove the higher codimension analogue of theorem 2.2.
There are two relevant observations. The first is Stallings's result [Reference Stallings21] that topological knots in $S^n$![]() of codimension greater than 2 are unknotted. In particular, the connected sum of knotted spheres in $S^{n+k}$
of codimension greater than 2 are unknotted. In particular, the connected sum of knotted spheres in $S^{n+k}$![]() is trivially well-defined if $k \ge 3$
is trivially well-defined if $k \ge 3$![]() . On the other hand, normal bundles do not exist in general for higher codimension (see, for instance, [Reference Hirsch13, Reference Rourke and Sanderson20]) so the proofs presented here cannot be generalized.
. On the other hand, normal bundles do not exist in general for higher codimension (see, for instance, [Reference Hirsch13, Reference Rourke and Sanderson20]) so the proofs presented here cannot be generalized.
Problem 4.2 Relative Annulus Conjecture
Prove the following conjecture. Suppose that $f, g \colon \! (S^{n+k}, S^{n}) \to ({\mathbb {R}}^{n+k +1}, {\mathbb {R}}^{n+1})$![]() are disjoint locally flat embeddings for which $f(S^{n+k})$
are disjoint locally flat embeddings for which $f(S^{n+k})$![]() is in the bounded component of ${\mathbb {R}}^{n+k+1} {\setminus} g(S^{n+k})$
is in the bounded component of ${\mathbb {R}}^{n+k+1} {\setminus} g(S^{n+k})$![]() . Then the submanifold of $({\mathbb {R}}^{n+k +1}, {\mathbb {R}}^{n+1})$
. Then the submanifold of $({\mathbb {R}}^{n+k +1}, {\mathbb {R}}^{n+1})$![]() that is bounded by $f(S^{n+k}, S^{n})$
that is bounded by $f(S^{n+k}, S^{n})$![]() and $g(S^{n+k}, S^{n})$
and $g(S^{n+k}, S^{n})$![]() is homeomorphic to $(S^{n+k}, S^n) \times [0,1]$
is homeomorphic to $(S^{n+k}, S^n) \times [0,1]$![]() .
.
Acknowledgments
I am especially grateful to Rob Kirby for discussing his work with me. One of his suggestions led to a significant simplification of the proof. Improvements are due to the contributions of Jim Davis, Mike Freedman, Kent Orr, Aru Ray, and Shida Wang. Thanks also go to a referee for several improvements.
This work was supported by a grant from the National Science Foundation, NSF-DMS-1505586.
Appendix A. Connected sums of submanifolds in the smooth category
Here we summarize the essential ingredient of the proof of the smooth version of theorem 3.2. The following result is a special case of Theorem [Reference Palais18, lemma 5.1].
Lemma A.1 Suppose that $U \subset {\mathbb {R}}^n$![]() is open set containing the origin and that $\psi \colon \! U \to {\mathbb {R}}^n$
is open set containing the origin and that $\psi \colon \! U \to {\mathbb {R}}^n$![]() is a differentiable map. If $\psi (0) = 0$
is a differentiable map. If $\psi (0) = 0$![]() and the derivative at $0$
and the derivative at $0$![]() satisfies $D\psi _0 = {\mathrm {Id}}$
satisfies $D\psi _0 = {\mathrm {Id}}$![]() , then there is a neighbourhood $V \subset U$
, then there is a neighbourhood $V \subset U$![]() of $0$
of $0$![]() and an isotopy $s \to \phi ^s$
and an isotopy $s \to \phi ^s$![]() of maps of ${\mathbb {R}}^n$
of maps of ${\mathbb {R}}^n$![]() for which: (1) $\phi ^0$
for which: (1) $\phi ^0$![]() is the identify; (2) $\phi ^s$
is the identify; (2) $\phi ^s$![]() is the identity off of $U$
is the identity off of $U$![]() for all $s$
for all $s$![]() ; and (3) $\phi ^1\big |_V = \psi \big |_V$
; and (3) $\phi ^1\big |_V = \psi \big |_V$![]() .
.
This is a consequence of [Reference Palais18, lemma 5.2]. Here is a statement with the notation slightly simplified.
Lemma A.2 Let $G$![]() a differentiable function from a neighbourhood of the origin in ${\mathbb {R}}^n$
a differentiable function from a neighbourhood of the origin in ${\mathbb {R}}^n$![]() to ${\mathbb {R}}^n$
to ${\mathbb {R}}^n$![]() satisfying $G(0) = 0$
satisfying $G(0) = 0$![]() and with the derivative at $0$
and with the derivative at $0$![]() satisfying $DG_0 = {\mathrm {Id}}$
satisfying $DG_0 = {\mathrm {Id}}$![]() . Then for every sufficiently small $r >0$
. Then for every sufficiently small $r >0$![]() there is a differentiable mapping $F\colon \! {\mathbb {R}}^n \times [0,1] \to {\mathbb {R}}^n$
there is a differentiable mapping $F\colon \! {\mathbb {R}}^n \times [0,1] \to {\mathbb {R}}^n$![]() for which
for which
(1) $F^s \colon \! x \to F(x, s)$
 is a diffeomorphism for all $s$
is a diffeomorphism for all $s$ .
.(2) $F^0$
 is the identity map.
is the identity map.(3) $F^s(x) = x$
 if $\|x\| > 2r$
if $\|x\| > 2r$ and $0 \le s \le 1$
and $0 \le s \le 1$ .
.(4) $F^1(x) = G(x)$
 if $\| x \| \le r$
if $\| x \| \le r$ .
.(5) $s \to F^s$
 is an isotopy.
is an isotopy.
The proof of this result is an explicit construction. First, the function $A(x)$![]() is defined by $G(x) = x + A(x)$
is defined by $G(x) = x + A(x)$![]() . Then a suitable smooth family of real-valued functions $\sigma _r(x)$
. Then a suitable smooth family of real-valued functions $\sigma _r(x)$![]() on ${\mathbb {R}}^n$
on ${\mathbb {R}}^n$![]() is defined. The isotopy $F(x,s)$
is defined. The isotopy $F(x,s)$![]() is given by the following.
is given by the following.

The proof that connected sums of submanifolds (of arbitrary codimension) is well-defined depends on relative versions of the previous two lemmas. That is, if $\phi$![]() and $G$
and $G$![]() in the two statements are function defined on pairs in $({\mathbb {R}}^n, {\mathbb {R}}^k)$
in the two statements are function defined on pairs in $({\mathbb {R}}^n, {\mathbb {R}}^k)$![]() , then an isotopy of maps of pairs is required. In this setting the isotopy $F(x,s)$
, then an isotopy of maps of pairs is required. In this setting the isotopy $F(x,s)$![]() above provides such a relative isotopy.
above provides such a relative isotopy.