A compactness result in the gradient theory of phase transitions

Abstract

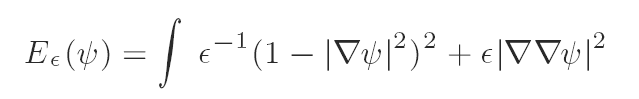We examine the singularly perturbed variational problem in the plane. As ε → 0, this functional favours |∇ψ| = 1 and penalizes singularities where |∇∇ψ| concentrates. Our main result is a compactness theorem: if {E_ε(ψ_ε)}_ε↓0 is uniformly bounded, then {∇ψ_ε}_ε↓0 is compact in L². Thus, in the limit ε → 0, ψ solves the eikonal equation |∇ψ| = 1 almost everywhere. Our analysis uses ‘entropy relations’ and the ‘div-curl lemma,’ adopting Tartar's approach to the interaction of linear differential equations and nonlinear algebraic relations.