Hostname: page-component-7479d7b7d-8zxtt Total loading time: 0 Render date: 2024-07-08T23:41:17.509Z Has data issue: false hasContentIssue false
  • English
  • Français

Compact and weakly compact Lipschitz operators

Part of: Special classes of linear operators Normed linear spaces and Banach spaces; Banach lattices Spaces with richer structures

Published online by Cambridge University Press:  11 May 2022

Arafat Abbar ,
Clément Coine  and
Colin Petitjean Open the ORCID record for Colin Petitjean [Opens in a new window]
Arafat Abbar
Affiliation:
Univ Gustave Eiffel, Univ Paris Est Creteil, CNRS, LAMA UMR8050, Marne-la-Vallée, France ([email protected], [email protected])
Clément Coine
Affiliation:
Normandie Univ, UNICAEN, CNRS, LMNO, 14000 Caen, France ([email protected])
Colin Petitjean
Affiliation:
Univ Gustave Eiffel, Univ Paris Est Creteil, CNRS, LAMA UMR8050, Marne-la-Vallée, France ([email protected], [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Any Lipschitz map $f : M \to N$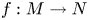 between two pointed metric spaces may be extended in a unique way to a bounded linear operator $\widehat {f} : \mathcal {F}(M) \to \mathcal {F}(N)$ 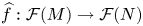between their corresponding Lipschitz-free spaces. In this paper, we give a necessary and sufficient condition for $\widehat {f}$ 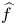to be compact in terms of metric conditions on $f$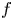. This extends a result by A. Jiménez-Vargas and M. Villegas-Vallecillos in the case of non-separable and unbounded metric spaces. After studying the behaviour of weakly convergent sequences made of finitely supported elements in Lipschitz-free spaces, we also deduce that $\widehat {f}$ 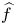is compact if and only if it is weakly compact.

Keywords

Compact operatorLipschitz-free spacelocally flat Lipschitz function

MSC classification

Primary: 46B50: Compactness in Banach (or normed) spaces 47B07: Operators defined by compactness properties
Secondary: 46B20: Geometry and structure of normed linear spaces 54E35: Metric spaces, metrizability
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 153 , Issue 3 , June 2023 , pp. 1002 - 1020
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abbar, A., Coine, C. and Petitjean, C.. On the dynamics of Lipschitz operators. Preprint arXiv:2011.10800, 2020.Google Scholar
Albiac, F., Ansorena, J., Cúth, M. and Doucha, M.. Lipschitz algebras and Lipschitz-free spaces over unbounded metric spaces. Preprint arXiv:2011.12993, 2020.Google Scholar
Albiac, F. and Kalton, N. J.. Lipschitz structure of quasi-Banach spaces. Isr. J. Math. 170 (2009), 317–335.10.1007/s11856-009-0031-zCrossRefGoogle Scholar
Albiac, F. and Kalton, N. J.. Topics in Banach space theory, 2nd edn, Graduate Texts in Mathematics, vol. 233 (Cham: Springer, 2016).CrossRefGoogle Scholar
Aliaga, R. J., Gartland, C., Petitjean, C. and Procházka, A.. Purely 1-unrectifiable spaces and locally flat Lipschitz functions. Preprint arXiv:2103.09370, 2021.Google Scholar
Aliaga, R. J. and Pernecká, E.. Supports and extreme points in Lipschitz-free spaces. Rev. Mat. Iberoam. 36 (2020), 2073–2089.CrossRefGoogle Scholar
Aliaga, R. J., Pernecká, E., Petitjean, C. and Procházka, A.. Supports in Lipschitz-free spaces and applications to extremal structure. J. Math. Anal. Appl. 489 (2020), 124128.CrossRefGoogle Scholar
Aliprantis, C. D. and Border, K. C.. Infinite dimensional analysis. A hitchhiker's guide, 3rd edn (Berlin: Springer, 2006).Google Scholar
Aliprantis, C. D. and Burkinshaw, O.. Positive operators. Pure and Applied Mathematics, vol. 119 (New York: Academic, 1985).Google Scholar
Cobzaş, Ş., Miculescu, R., Radu, and Nicolae, A.. Lipschitz functions. Lecture Notes in Mathematics, vol. 2241 (Cham: Springer, 2019).CrossRefGoogle Scholar
Cabrera-Padilla, M. G. and Jiménez-Vargas, A.. A new approach on Lipschitz compact operators. Topol. Appl. 203 (2016), 22–31.CrossRefGoogle Scholar
Godefroy, G. and Kalton, N. J.. Lipschitz-free Banach spaces. Stud. Math. 159 (2003), 121–141.CrossRefGoogle Scholar
Hájek, P., Lancien, G., Pernecká, E.. Approximation and Schur properties for Lipschitz free spaces over compact metric spaces. Bull. Belg. Math. Soc. Simon Stevin 23 (2016), 63–72.CrossRefGoogle Scholar
Jiménez-Vargas, A.. Weakly compact composition operators on spaces of Lipschitz functions. Positivity 19 (2015), 807–815.CrossRefGoogle Scholar
Jiménez-Vargas, A., Sepulcre, J. M. and Villegas-Vallecillos, J. M. M.. Lipschitz compact operators. J. Math. Anal. Appl. 415 (2014), 889–901.CrossRefGoogle Scholar
Jiménez-Vargas, A. and Villegas-Vallecillos, M.. Compact composition operators on noncompact Lipschitz spaces. J. Math. Anal. Appl. 398 (2013), 221–229.CrossRefGoogle Scholar
Kamowitz, H. and Scheinberg, S.. Some properties of endomorphisms of Lipschitz Algebras. Stud. Math. 96 (1990), 61–67.CrossRefGoogle Scholar
Kalton, N. J.. Spaces of Lipschitz and Hölder functions and their applications. Collect. Math. 55 (2004), 171–217.Google Scholar
Megginson, R. E.. An introduction to banach space theory (New York: Springer, 1998).CrossRefGoogle Scholar
Weaver, N.. Lipschitz algebras, 2nd edn (River Edge, NJ: World Scientific Publishing Co., 2018).CrossRefGoogle Scholar