Classification of regularly solvable first-order differential operators

Synopsis

In this article the expression τφ: = pφ + qφ with complex-valued coefficients is considered. We are particularly concerned with this expression when it is not formally symmetric, i.e., τ ≠ τ⁺, where τ⁺ is the formal adjoint of τ, and especially with the operators which are regularly solvable with respect to the minimal operators generated by τ and τ⁺ in the sense of W. D. Evans in [3]. This article is divided into five sections: Section 1 is an introduction, Section 2 is a brief study of the regular problem, in Section 3, some preliminary results in the singular case are displayed in Section 4, the joint field of regularity in the singular case is investigated and in Section 5, we discuss the case when 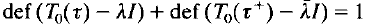.