Chevalley's theorem in class C^r

Abstract

Let W be a finite reflection group acting orthogonally on ℝⁿ, P be the Chevalley polynomial mapping determined by an integrity basis of the algebra of W-invariant polynomials, and h be the highest degree of the coordinate polynomials in P. Let r be a positive integer and [r/h] be the integer part of r/h. There exists a linear mapping 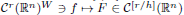such that f = F ∘ P, which is continuous for the natural Fréchet topologies. A general counter-example shows that this result is the best possible. The proof uses techniques of division by linear forms and a study of compensation phenomena. An extension to P⁻¹(ℝⁿ) of invariant formally holomorphic regular fields is needed.