No CrossRef data available.
Article contents
Cavitation of a spherical body under mechanical and self-gravitational forces
Published online by Cambridge University Press: 08 January 2024
Abstract
In this paper, we look for minimizers of the energy functional for isotropic compressible elasticity taking into consideration the effect of a gravitational field induced by the body itself. We consider two types of problems: the displacement problem in which the outer boundary of the body is subjected to a Dirichlet-type boundary condition, and the one with zero traction on the boundary but with an internal pressure function. For a spherically symmetric body occupying the unit ball $\mathcal {B}\in \mathbb {R}^3$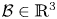 , the minimization is done within the class of radially symmetric deformations. We give conditions for the existence of such minimizers, for satisfaction of the Euler–Lagrange equations, and show that for large displacements or large internal pressures, the minimizer must develop a cavity at the centre. We discuss a numerical scheme for approximating the minimizers for the displacement problem, together with some simulations that show the dependence of the cavity radius and minimum energy on the displacement and mass density of the body.
, the minimization is done within the class of radially symmetric deformations. We give conditions for the existence of such minimizers, for satisfaction of the Euler–Lagrange equations, and show that for large displacements or large internal pressures, the minimizer must develop a cavity at the centre. We discuss a numerical scheme for approximating the minimizers for the displacement problem, together with some simulations that show the dependence of the cavity radius and minimum energy on the displacement and mass density of the body.
- Type
- Research Article
- Information
- Copyright
- Copyright © The Author(s), 2024. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh



