Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Winkler, Michael
2014.
Global asymptotic stability of constant equilibria in a fully parabolic chemotaxis system with strong logistic dampening.
Journal of Differential Equations,
Vol. 257,
Issue. 4,
p.
1056.
Yokota, Tomomi
Winkler, Michael
Ito, Akio
and
Fujie, Kentarou
2015.
Stabilization in a chemotaxis model for tumor invasion.
Discrete and Continuous Dynamical Systems,
Vol. 36,
Issue. 1,
p.
151.
Li, Yuhuan
Lin, Ke
and
Mu, Chunlai
2015.
Boundedness and asymptotic behavior of solutions to a chemotaxis–haptotaxis model in high dimensions.
Applied Mathematics Letters,
Vol. 50,
Issue. ,
p.
91.
Bellomo, N.
Bellouquid, A.
Tao, Y.
and
Winkler, M.
2015.
Toward a mathematical theory of Keller–Segel models of pattern formation in biological tissues.
Mathematical Models and Methods in Applied Sciences,
Vol. 25,
Issue. 09,
p.
1663.
Tao, Youshan
and
Winkler, Michael
2015.
Large Time Behavior in a Multidimensional Chemotaxis-Haptotaxis Model with Slow Signal Diffusion.
SIAM Journal on Mathematical Analysis,
Vol. 47,
Issue. 6,
p.
4229.
Li, Yan
and
Lankeit, Johannes
2016.
Boundedness in a chemotaxis–haptotaxis model with nonlinear diffusion.
Nonlinearity,
Vol. 29,
Issue. 5,
p.
1564.
Wang, Yifu
2016.
Boundedness in the higher-dimensional chemotaxis–haptotaxis model with nonlinear diffusion.
Journal of Differential Equations,
Vol. 260,
Issue. 2,
p.
1975.
Hu, Xuegang
Wang, Liangchen
Mu, Chunlai
and
Li, Ling
2016.
Boundedness in a three-dimensional chemotaxis–haptotaxis model with nonlinear diffusion.
Comptes Rendus. Mathématique,
Vol. 355,
Issue. 2,
p.
181.
Wang, Yifu
and
Ke, Yuanyuan
2016.
Large time behavior of solution to a fully parabolic chemotaxis–haptotaxis model in higher dimensions.
Journal of Differential Equations,
Vol. 260,
Issue. 9,
p.
6960.
Zheng, Jiashan
and
Wang, Yifu
2016.
Boundedness of solutions to a quasilinear chemotaxis–haptotaxis model.
Computers & Mathematics with Applications,
Vol. 71,
Issue. 9,
p.
1898.
Cao, Xinru
2016.
Boundedness in a three-dimensional chemotaxis–haptotaxis model.
Zeitschrift für angewandte Mathematik und Physik,
Vol. 67,
Issue. 1,
Stinner, Christian
Surulescu, Christina
and
Uatay, Aydar
2016.
Global existence for a go-or-grow multiscale model for tumor invasion with therapy.
Mathematical Models and Methods in Applied Sciences,
Vol. 26,
Issue. 11,
p.
2163.
Zheng, Jiashan
2017.
Boundedness of the solution of a higher-dimensional parabolic–ODE–parabolic chemotaxis–haptotaxis model with generalized logistic source.
Nonlinearity,
Vol. 30,
Issue. 5,
p.
1987.
Zheng, Jiashan
2017.
Boundedness of solutions to a quasilinear higher-dimensional chemotaxis-haptotaxis model with nonlinear diffusion.
Discrete & Continuous Dynamical Systems - A,
Vol. 37,
Issue. 1,
p.
627.
Wang, Liangchen
Mu, Chunlai
Hu, Xuegang
and
Tian, Ya
2017.
Boundedness in a quasilinear chemotaxis‐haptotaxis system with logistic source.
Mathematical Methods in the Applied Sciences,
Vol. 40,
Issue. 8,
p.
3000.
Pang, Peter Y.H.
and
Wang, Yifu
2017.
Global existence of a two-dimensional chemotaxis–haptotaxis model with remodeling of non-diffusible attractant.
Journal of Differential Equations,
Vol. 263,
Issue. 2,
p.
1269.
Liu, Ji
and
Wang, Yifu
2017.
A quasilinear chemotaxis–haptotaxis model: The roles of nonlinear diffusion and logistic source.
Mathematical Methods in the Applied Sciences,
Vol. 40,
Issue. 6,
p.
2107.
Winkler, Michael
2018.
Finite-time blow-up in low-dimensional Keller–Segel systems with logistic-type superlinear degradation.
Zeitschrift für angewandte Mathematik und Physik,
Vol. 69,
Issue. 2,
Ke, Yuanyuan
and
Zheng, Jiashan
2018.
A note for global existence of a two-dimensional chemotaxis–haptotaxis model with remodeling of non-diffusible attractant.
Nonlinearity,
Vol. 31,
Issue. 10,
p.
4602.
Pang, Peter Y. H.
and
Wang, Yifu
2018.
Global boundedness of solutions to a chemotaxis–haptotaxis model with tissue remodeling.
Mathematical Models and Methods in Applied Sciences,
Vol. 28,
Issue. 11,
p.
2211.
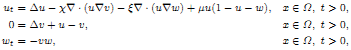
 there exists a positive constant μ* depending only on χ, ξ, Ω, u0 and w0 such that for any μ < μ* the above global solution (u, v, w) approaches the spatially uniform state (1, 1, 0) as time goes to infinity.
there exists a positive constant μ* depending only on χ, ξ, Ω, u0 and w0 such that for any μ < μ* the above global solution (u, v, w) approaches the spatially uniform state (1, 1, 0) as time goes to infinity.

