Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-27T06:07:40.635Z Has data issue: false hasContentIssue false
  • English
  • Français

Blow-up behaviour for nonlinearly perturbed semilinear parabolic equations

Published online by Cambridge University Press:  14 November 2011

Stephen Bricher
Stephen Bricher
Affiliation:
Department of Mathematics, Linfield College, McMinnville. OR 97128, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Extract

The blow-up behaviour of radially symmetric classical solutions to the quasilinear parabolic equation

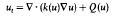
is analysed assuming k(u) and Q(u) are small perturbations of {k, Q} ≡ {1, up},p > 1. Moreover, it is proved that the asymptotic behaviour near blowup of solutions to the semilinear equation ut = Δu + up, and in particular the final-time profile, is stable with respect to small quasilinear perturbations of the elliptic operator.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 124 , Issue 5 , 1994 , pp. 947 - 969
Copyright
Copyright © Royal Society of Edinburgh 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Bebernes, J. and Bricher, S.. Final time blowup profiles for semilinear parabolic equations via center manifold theory. SIAM J. Math. Anal. 23 (1992), 852–869.CrossRefGoogle Scholar
2Bebernes, J., Bricher, S. and Galaktionov, V. A.. Asymptotics of blowup for weakly quasilinear parabolic problems. Nonlinear Anal, (to appear).Google Scholar
3Bebernes, J. and Eberly, D.. Mathematical Problems from Combustion Theory, Appl. Math. Sci. 83 (Berlin: Springer, 1989).Google Scholar
4Bressan, A.. Stable blowup patterns. J. Differential Equations 98 (1992), 57–75.CrossRefGoogle Scholar
5DiBenedetto, E.. Continuity of weak solutions to a general porous medium equation. Indiana Univ. Math. 3 32(1983), 83–119.CrossRefGoogle Scholar
6Filippas, S. and Kohn, R. V.. Refined asymptotics for the blowup of ut – Δu = up. Comm. Pure Appl. Math. 45(1992), 821–869.Google Scholar
7Friedman, A.. Partial Differential Equations of Parabolic Type (Englewood Cliffs, NJ: Prentice Hall, 1964).Google Scholar
8Friedman, A. and McLeod, B.. Blow-up of positive solutions of semilinear heat equations. Indiana Univ. Math. J. 34 (1985), 425–447.CrossRefGoogle Scholar
9Galaktionov, V. A.. On asymptotic self-similar behaviour for quasilinear heat equation: global blowup (preprint).Google Scholar
10Galaktionov, V. A.. On asymptotic self-similar behaviour for quasilinear heat equation: single point blowup (preprint).Google Scholar
11Galaktionov, V. A., Herrero, M. A. and Velázquez, J. J. L.. The space structure near a blow-up point for semilinear heat equations: a formal approach. Z. Vychisl. Matem. i Matem. Fiz. 31 (1991), 399–411.Google Scholar
12Galaktionov, V. A. and Posashkov, S. A.. Applications of new comparison theorems for unbounded solutions of a nonlinear parabolic equation. Differentsial'nye Uravneniya 22 (1986), 1165–1173.Google Scholar
13Galaktionov, V. A. and Posashkov, S. S.. Estimates of localized unbounded solutions of quasilinear parabolic equations. Differentsial'nye Uravneniya 23 (1987), 1133–1143.Google Scholar
14Galaktionov, V. A. and Posashkov, S. S.. On some method to investigate unbounded solutions of quasilinear parabolic equations. Z. Vychisl. Matem. i Matem. Fiz. 28 (1988), 842–854.Google Scholar
15Galaktionov, V. A. and Posashkov, S. S.. On new explicit solutions of parabolic equations with quadratic nonlinearities. Z. Vychisl. Matem. i Matem. Fiz. 29 (1989), 497–506.Google Scholar
16Galaktionov, V. A. and Posashkov, S. S.. Any large solution of a nonlinear heat conduction equation becomes monotone in time. Proc. Roy. Soc. Edinburgh Sect. A 118 (1991), 13–20.CrossRefGoogle Scholar
17Galaktionov, V. A. and Vazquez, J. L.. Asymptotic behaviour of nonlinear parabolic equations with critical exponents. A dynamical systems approach. J. Fund. Anal. 100 (1991), 435–462.CrossRefGoogle Scholar
18Galaktionov, V. A. and Vazquez, J. L.. Regional blow-up in a semilinear heat equation with convergence to a Hamilton–Jacobi equation. SIAM J. Math. Anal. 24 (1993), 1254–1276.Google Scholar
19Galaktionov, V. A. and Vazquez, J. L.. Extinction for a quasilinear heat equation with absorption II. A dynamical systems approach (preprint).Google Scholar
20Herrero, M. A. and Velázquez, J. J. L.. Blow-up behavior of one-dimensional semilinear parabolic equations. Ann. Inst. H. Poincaré Anal. Nonlinéaire 10 (1993), 131–189.Google Scholar
21Herrero, M. A. and Velázquez, J. J. L.. Blow-up profiles in one-dimensional semilinear parabolic problems. Comm. in Partial Differential Equations 17 (1992), 205–219.Google Scholar
22Langlais, M. and Phillips, D.. Stabilization of solutions of nonlinear and degenerate evolution equations. Nonlinear Anal. 9 (1985), 321–333.Google Scholar
23Samarskii, A. A., Galaktionov, V. A., Kurdyumov, S. P. and Mikhailov, A. P.. Blow-Up in Problems for Quasilinear Parabolic Equations (Moscow: Nauka, 1987 (Russian); English translation: Berlin: Walter de Gruyter (to appear)).Google Scholar