Article contents
Baer semigroup coordinatisations of distributive lattices
Published online by Cambridge University Press: 14 November 2011
Synopsis
In a previous publication we investigated certain idempotent residuated mappings and showed how these could be used to provide a solution to the problem of finding a Baer semigroup coordinatisation of bounded modular lattices. Here we use essentially the same idempotents to provide a coordinatisation of bounded distributive lattices. Specifically, we prove that a bounded lattice L is distributive if and only if it can be coordinatised by a Baer semigroup S such that if eS, fS, gS ∈ R(S) with eS ∩ fS = eS ∩ gS then there are idempotents ē, 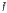 ,
, 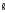 ∈ S such that ēS = eS,
∈ S such that ēS = eS, 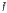 S = fS,
S = fS, 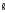 S = gS and ē commutes with both
S = gS and ē commutes with both 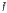 and
and 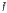 .
.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 85 , Issue 3-4 , 1980 , pp. 307 - 312
- Copyright
- Copyright © Royal Society of Edinburgh 1980
References
- 1
- Cited by


