Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Sacks, Paul E.
1991.
Limiting Behavior of Solutions of $\bf u_t=\D u^m$ as $\bf m\to\infty$.
Rocky Mountain Journal of Mathematics,
Vol. 21,
Issue. 2,
Hui, Kin Ming
1995.
Singular limit of solutions of 𝑢_{𝑡}=Δ𝑢^{𝑚}-𝐴⋅∇(𝑢^{𝑞}/𝑞) as 𝑞→∞.
Transactions of the American Mathematical Society,
Vol. 347,
Issue. 5,
p.
1687.
Dafermos, Constantine M.
2000.
Hyperbolic Conservation Laws in Continuum Physics.
Vol. 325,
Issue. ,
p.
209.
2005.
Hyberbolic Conservation Laws in Continuum Physics.
Vol. 325,
Issue. ,
p.
511.
Hui, Kin Ming
and
Kim, Sunghoon
2020.
Singular Limit of the Generalized Burgers Equation with Absorption.
Journal of Dynamics and Differential Equations,
Vol. 32,
Issue. 2,
p.
809.
Liu, Jian-Guo
and
Xu, Xiangsheng
2021.
Existence and Incompressible Limit of a Tissue Growth Model with Autophagy.
SIAM Journal on Mathematical Analysis,
Vol. 53,
Issue. 5,
p.
5215.


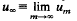 exists and satisfies the stationary equation
exists and satisfies the stationary equation