Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-28T14:15:11.106Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic behaviour as p → ∞ of least energy solutions of a (p, q(p))-Laplacian problem

Part of: Partial differential equations Linear function spaces and their duals Elliptic equations and systems Representations of solutions

Published online by Cambridge University Press:  17 January 2019

C. O. Alves ,
G. Ercole  and
G. A. Pereira
C. O. Alves
Affiliation:
Universidade Federal de Campina Grande, Campina Grande, PB 58.109-970, Brazil ([email protected])
G. Ercole
Affiliation:
Universidade Federal de Minas Gerais, Belo Horizonte, MG 30.123-970, Brazil ([email protected]; [email protected])
G. A. Pereira
Affiliation:
Universidade Federal de Minas Gerais, Belo Horizonte, MG 30.123-970, Brazil ([email protected]; [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the asymptotic behaviour, as p → ∞, of the least energy solutions of the problem

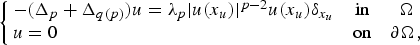$$\left\{ {\matrix{ {-(\Delta _p + \Delta _{q(p)})u = \lambda _p \vert u(x_u) \vert ^{p-2}u(x_u)\delta _{x_u}} & {{\rm in}} & \Omega \cr {u = 0} \hfill \hfill \hfill & {{\rm on}} & {\partial \Omega ,} \cr } } \right.$$
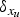where xu is the (unique) maximum point of |u|, $\delta _{x_{u}}$ is the Dirac delta distribution supported at xu,
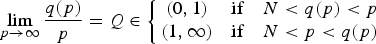$$\mathop {\lim }\limits_{p\to \infty } \displaystyle{{q(p)} \over p} = Q\in \left\{ {\matrix{ {(0,1)} & {{\rm if}} & {N < q(p) < p} \cr {(1,\infty )} & {{\rm if}} & {N < p < q(p)} \cr } } \right.$$
and λp > 0 is such that
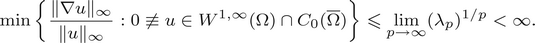$$\min \left\{ {\displaystyle{{{\rm \Vert }\nabla u{\rm \Vert }_\infty } \over {{\rm \Vert }u{\rm \Vert }_\infty }}:0 \ne u\in W^{1,\infty }(\Omega )\cap C_0(\bar{\Omega })} \right\} \les \mathop {\lim }\limits_{p\to \infty } (\lambda _p)^{1/p} < \infty .$$

Keywords

Asymptotic behaviourdirac deltainfinity LaplacianNehari setviscosity solution

MSC classification

Primary: 35B40: Asymptotic behavior of solutions
Secondary: 35D40: Viscosity solutions 35J20: Variational methods for second-order elliptic equations 35J92: Quasilinear elliptic equations with $p$-Laplacian 46E35: Sobolev spaces and other spaces of “smooth” functions, embedding theorems, trace theorems
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 149 , Issue 6 , December 2019 , pp. 1493 - 1522
Copyright
Copyright © Royal Society of Edinburgh 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Banach, S.. Theory of linear operations, vol. 38 (Amsterdam: Elsevier, 1987).Google Scholar
2Barles, G. and Busca, J.. Existence and comparison results for fully nonlinear degenerate elliptic equations without zeroth-order term. Comm. Part. Diff. Equ. 26 (2001), 2323–2337.Google Scholar
3Bocea, M. and Mihăilescu, M.. Existence of nonnegative viscosity solutions for a class of problems involving the ∞-Laplacian. NoDEA Nonlinear Differ. Equ. Appl. 23 (2016), 21 Art. 11.Google Scholar
4Charro, F. and Peral, I.. Limits branch of solutions as p → ∞ for a family of subdiffusive problems related to the p-Laplacian. Comm. Part. Diff. Equ. 32 (2007), 1965–1981.Google Scholar
5Charro, F. and Parini, E.. Limits as p → ∞ of p-Laplacian problems with a superdiffusive power-type nonlinearity: positive and sign-changing solutions. J. Math. Anal. Appl. 372 (2010), 629–644.Google Scholar
6Charro, F. and Parini, E.. Limits as p → ∞ of p-Laplacian eigenvalue problems perturbed with a concave or convex term. Calc. Var. Partial Differ. Equ. 46 (2013), 403–425.Google Scholar
7Crandall, M. G., Evans, L. C. and Gariepy, R. F.. Optimal Lipschitz extensions and the infinity Laplacian. Calc. Var. Partial Differ. Equ. 13 (2001), 123–139.Google Scholar
8da Silva, J. V., Rossi, J. D. and Salort, A. M.. Maximal solutions for the ∞-eigenvalue problem. Adv. Calc. Var. (to appear). https://doi.org/10.1515/acv-2017-0024Google Scholar
9Ercole, G. and Pereira, G.. Asymptotics for the best Sobolev constants and their extremal functions. Math. Nachr. 289 (2016), 1433–1449.Google Scholar
10Fukagai, N., Ito, M. and Narukawa, K.. Limit as p → ∞ of p-Laplace eigenvalue problems and L ∞-inequality of the Poincaré type. Differ. Integral Equ. 12 (1999), 183–206.Google Scholar
11Hynd, R. and Lindgren, E.. Extremal functions for Morrey's inequality in convex domains. Math. Ann. (2018) https://doi.org/10.1007/s00208-018-1775-8.Google Scholar
12Jensen, R.. Uniqueness of Lipschitz extensions: minimizing the sup norm of the gradient. Arch. Rational Mech. Anal. 123 (1993), 51–74.Google Scholar
13Juutinen, P., Lindqvist, P. and Manfredi, J.. The ∞-eigenvalue problem. Arch. Ration. Mech. Anal. 148 (1999), 89–105.Google Scholar
14Lindqvist, P.. Notes on the infinity Laplace equation. BCAM SpringerBriefs in Mathematics (Bilbao: Springer, 2016).Google Scholar
15Lindqvist, P. and Manfredi, J.. The Harnack inequality for ∞-harmonic functions. Electron. J. Differ. Equ. 4 (1995), 1–5.Google Scholar