Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-12-04T19:45:39.418Z Has data issue: false hasContentIssue false
  • English
  • Français

The approximation of exterior Neumann problems in a halfspace by means of problems with compact boundary

Published online by Cambridge University Press:  14 November 2011

Ronald I. Becker  and
Ronald New
Ronald I. Becker
Affiliation:
Department of Mathematics, University of Cape Town, Rondebosch 7700, South Africa
Ronald New
Affiliation:
Central Acoustics Laboratory, University of Cape Town, Rondebosch 7700, South Africa
Get access Rights & Permissions [Opens in a new window]

Synopsis

This paper describes a proof that the solutions of Neumann problems for the exterior of spheres {x ∊ ℝ3∣ 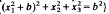converge to the solutions of the exterior problem for the halfspace {x ∊ ℝ3 } x1 ≧ 0} as b → ∞ provided that the boundary data converge in a certain sense. The method requires that there be some dissipation which can be arbitrarily small. Fredholm integral equations are set up for the boundary data, and these are solved by means of Neumann series for large b. Estimates on the terms of the series (which involve singular integrals), in terms of b, allow the convergence proof to be carried through.

The procedure of expressing problems with infinite boundaries in terms of problems with finite boundaries allows the implementation of an effective numerical procedure for determining, for example, the entire near-field of a baffled piston, a problem whose solution has proved elusive for many years.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 111 , Issue 3-4 , 1989 , pp. 285 - 300
Copyright
Copyright © Royal Society of Edinburgh 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Atkinson, F. V.. Discrete and continuous boundary value problems (New York: Academic Press, 1964).Google Scholar
2Becker, R. I. and New, R.. On the approximation of exterior Neumann problems for infinite boundaries by problems with finite boundaries (International Symposium on Underwater Acoustics, Tel-Aviv, June 1981).Google Scholar
3Kellogg, O. D.. Foundations of Potential Theory (Berlin: Springer, 1929).CrossRefGoogle Scholar
4New, R.. A limiting form for the nearfield of the baffled piston. J. Acoust. Soc. Amer. Suppl. 1 (Proceedings of ASA) 69 (1981), S60.CrossRefGoogle Scholar
5New, R., Becker, R. I. and Wilhelmij, P.. A limiting form for the nearfield of the baffled piston. J. Acoust. Soc. Amer. 70 (1981), 1518–1526.CrossRefGoogle Scholar
6Smirnov, V. I.. A Course of Higher Mathematics, Vol. 4 (London: Pergamon, 1964).Google Scholar
7Sneddon, I. N.. Elements of Partial Differential Equations (New York: McGraw-Hill, 1957).Google Scholar
8Titchmarsh, E. C.. Eigenfunction Expansions (London: Oxford University Press, 1946).Google Scholar
9Titchmarsh, E. C.. Eigenfunction Expansions, Part II (London: Oxford University Press, 1958).Google Scholar
10Weyl, H.. Ueber gewöhnliche lineare Differentialgleichungen mit Singularen Stellen und ihre Eigenfunktionen. Göttinger Nachrichten (1909), 37–64.Google Scholar
11Wilcox, C. H.. A generalization of theorems of Rellich and Atkinson. Proc. Amer. Math. Soc. 7 (1956), 271–276.CrossRefGoogle Scholar
12Greenspan, M.. Piston radiator: Some extensions of the theory. J. Acoust. Soc. Amer. 65 (1979), 608–521.CrossRefGoogle Scholar