Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hinton, D B
Klaus, M
and
Shaw, J K
1989.
High-energy asymptotics for the scattering matrix on the line.
Inverse Problems,
Vol. 5,
Issue. 6,
p.
1049.
Rybkin, Alexei
2004.
Spectral Methods for Operators of Mathematical Physics.
p.
185.
Avdonin, Sergei
Mikhaylov, Victor
and
Rybkin, Alexei
2007.
The Boundary Control Approach to the Titchmarsh-Weyl m–Function. I. The Response Operator and the A–Amplitude.
Communications in Mathematical Physics,
Vol. 275,
Issue. 3,
p.
791.
Boumenir, Amin
and
Vu, Kim Tuan
2007.
The interpolation of the Titchmarsh–Weyl function.
Journal of Mathematical Analysis and Applications,
Vol. 335,
Issue. 1,
p.
72.
Luger, Annemarie
Teschl, Gerald
and
Wöhrer, Tobias
2016.
Asymptotics of the Weyl function for Schrödinger operators with measure-valued potentials.
Monatshefte für Mathematik,
Vol. 179,
Issue. 4,
p.
603.



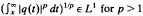 we calculate the Titchmarsh-Weyl
we calculate the Titchmarsh-Weyl 