Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-01-12T22:37:55.425Z Has data issue: false hasContentIssue false
  • English
  • Français

An ergodic theorem for asymptotically nonexpansive mappings

Published online by Cambridge University Press:  14 November 2011

Manfred Krüppel  and
Jaroslaw Górnicki
Manfred Krüppel
Affiliation:
Universität Rostock, Auβenstelle Güstrow, Fachbereich Mathematik, Goldberger Str. 12, O-2600 Güstrow, Germany
Jaroslaw Górnicki
Affiliation:
Department of Mathematics, Rzeszów Technical University, P.O. Box 85, 35-959 Rzeszów, Poland
Get access Rights & Permissions [Opens in a new window]

Abstract

The purpose of this paper is to prove the following (nonlinear) mean ergodic theorem: Let E be a uniformly convex Banach space, let C be a nonempty bounded closed convex subset of E and let T: C → C be an asymptotically nonexpansive mapping. If

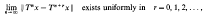
exists uniformly in r = 0, 1, 2,…, then the sequence {Tnx} is strongly almost-convergent to a fixed point y of T, that is,

uniformly in i = 0, 1, 2, ….

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 124 , Issue 1 , 1994 , pp. 23 - 31
Copyright
Copyright © Royal Society of Edinburgh 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Baillon, J. B.. Un thèorème de type ergodique pour les contractions non linéaires dans un espace de Hilbert. C. R. Acad. Sci. Paris Sèr. I Math. 280 (1975), A1511–A1514.Google Scholar
2Baillon, J. B.. Quelques propèrtiès de convergence asymptotique pour les contractions impaires. C. R. Acad. Sci. Paris Sèr. I Math. 283 (1976), A587–A590.Google Scholar
3Baillon, J. B.. Quelques aspects de la théorie des points fixes dans les espaces de Banach I, II. (Seminaire d'Analyse Fonctionnelle 1978–1979, École Polytechnique, Centre de Mathématiques, Exposé 7, 8, November 1978.)Google Scholar
4Baillon, J. B., Bruck, R. E. and Reich, S.. On the asymptotic behavior of nonexpansive mappings and semigroups in Banach spaces. Houston J. Math. 4 (1978), 1–9.Google Scholar
5Bruck, R. E.. On the almost-convergence of iterates of a nonexpansive mapping in Hilbert space and the structure of the weak ω-limit set. Israel J. Math. 29 (1978), 1–16.CrossRefGoogle Scholar
6Bruck, R. E.. On the convex approximation property and the asymptotic behavior of nonlinear contractions in Banach spaces. Israel J. Math. 38 (1981), 304–314.CrossRefGoogle Scholar
7Goebel, K. and Kirk, W. A.. A fixed point theorem for asymptotically nonexpansive mappings. Proc. Amer. Math. Soc. 35 (1972), 171–174.Google Scholar
8Kobayasi, K. and Miyadera, I.. On the strong convergence of the Cesaro means of contractions in Banach spaces. Proc. Japan Acad. Ser. A 56 (1980), 245–249.Google Scholar
9Lorentz, G. G.. A contribution to the theory of divergent sequences. Acta Math. 80 (1948), 167–190.CrossRefGoogle Scholar
10Reich, S.. Almost convergence and nonlinear ergodic theorems. J. Approx. Theory 24 (1978), 269–272.Google Scholar