Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-16T01:16:53.008Z Has data issue: false hasContentIssue false
  • English
  • Français

A uniqueness result for a singular elliptic equation with gradient term

Part of: Elliptic equations and systems Partial differential equations

Published online by Cambridge University Press:  22 June 2018

José Carmona  and
Tommaso Leonori
José Carmona
Affiliation:
Departamento de Matemáticas, Universidad de Almería, Carretera Sacramento S/N, La Cañada de San Urbano, 04120 Almería, Spain ([email protected])
Tommaso Leonori
Affiliation:
Departamento de Análisis Matemático, Campus Fuentenueva S/N, Universidad de Granada, 18071 Granada, Spain ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove the uniqueness of a solution for a problem whose simplest model is

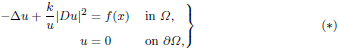
with k ≥ 1, 0 f ∈ L∞(Ω) and Ω is a bounded domain of ℝN, N ≥ 2. So far, uniqueness results are known for k < 1, while existence holds for any k ≥ 1 and f positive in open sets compactly embedded in a neighbourhood of the boundary. We extend the uniqueness results to the k ≥ 1 case and show, with an example, that existence does not hold if f is zero near the boundary. We even deal with the uniqueness result when f is replaced by a nonlinear term λuq with 0 < q < 1 and λ > 0.

Keywords

nonlinear elliptic equationssingular natural growth gradient termscomparison principle

MSC classification

Primary: 35J65: Nonlinear boundary value problems for linear elliptic equations 35J75: Singular elliptic equations
Secondary: 35A02: Uniqueness problems
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 148 , Issue 5 , October 2018 , pp. 983 - 994
Copyright
Copyright © Royal Society of Edinburgh 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

*

Present address: Dipartimento di Scienze di Base e Applicate per l'Ingegneria ‘Sapienza’, Università di Roma I, Via Antonio Scarpa 10, 00161 Roma, Italy ([email protected]).