The symmetric cross-cap number of the groups Cm × Dn
Published online by Cambridge University Press: 12 November 2008
Abstract
Every finite group G acts as an automorphism group of some non-orientable Klein surfaces without boundary. The minimal genus of these surfaces is called the symmetric cross-cap number and denoted by 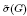 . This number is related to other parameters defined on surfaces as the symmetric genus and the strong symmetric genus.
. This number is related to other parameters defined on surfaces as the symmetric genus and the strong symmetric genus.
The systematic study of the symmetric cross-cap number was begun by C. L. May, who also calculated it for certain finite groups. Here we obtain the symmetric cross-cap number for the groups Cm × Dn. As an application of this result, we obtain arithmetic sequences of integers which are the symmetric cross-cap number of some group. Finally, we recall the several different genera of the groups Cm × Dn.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 138 , Issue 6 , December 2008 , pp. 1197 - 1213
- Copyright
- Copyright © Royal Society of Edinburgh 2008
- 7
- Cited by


