Hostname: page-component-f554764f5-rvxtl Total loading time: 0 Render date: 2025-04-21T09:59:21.378Z Has data issue: false hasContentIssue false
  • English
  • Français

Robustness of nonuniform mean-square exponential dichotomies

Part of: Stochastic analysis Stability theory

Published online by Cambridge University Press:  18 April 2023

Hailong Zhu Open the ORCID record for Hailong Zhu [Opens in a new window]
Hailong Zhu*
Affiliation:
Anhui University of Finance and Economics, Bengbu 233030, China ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

For linear stochastic differential equations with bounded coefficients, we establish the robustness of nonuniform mean-square exponential dichotomy (NMS-ED) on $[t_{0},\,+\infty )$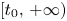, $(-\infty,\,t_{0}]$ 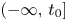and the whole ${\Bbb R}$ 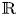separately, in the sense that such an NMS-ED persists under a sufficiently small linear perturbation. The result for the nonuniform mean-square exponential contraction is also discussed. Moreover, in the process of proving the existence of NMS-ED, we use the observation that the projections of the ‘exponential growing solutions’ and the ‘exponential decaying solutions’ on $[t_{0},\,+\infty )$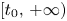, $(-\infty,\,t_{0}]$ 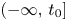and ${\Bbb R}$ 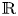are different but related. Thus, the relations of three types of projections on $[t_{0},\,+\infty )$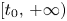, $(-\infty,\,t_{0}]$ 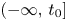and ${\Bbb R}$ 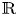are discussed.

Keywords

robustnessnonuniform mean-square exponential contractionnonuniform mean-square exponential dichotomystochastic differential equations

MSC classification

Primary: 60H10: Stochastic ordinary differential equations
Secondary: 34D09: Dichotomy, trichotomy
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 154 , Issue 2 , April 2024 , pp. 525 - 567
Check for updates
Copyright
Copyright © The Author(s), 2023. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Barreira, L. and Pesin, Ya.. Lyapunov exponents and smooth ergodic theory. University Lecture Series, vol. 23 (American Mathematical Society, 2002). http://www.ams.org/books/ulect/023/Google Scholar
Barreira, L. and Pesin, Ya.. Nonuniform hyperbolicity. Encyclopedia of Mathematics and its Application, vol. 115 (Cambridge University Press, 2007). https://www.cambridge.org/core/books/nonuniform-hyperbolicity/985F811D19CABAE5D0DF0C59BFBFFF18Google Scholar
Barreira, L., Chu, J. and Valls, C.. Robustness of nonuniform dichotomies with different growth rates. São Paulo J. Math. Sci 5 (2011), 203–231.Google Scholar
Barreira, L., Chu, J. and Valls, C.. Lyapunov functions for general nonuniform dichotomies. Milan J. Math. 81 (2013), 153–169.Google Scholar
Barreira, L., Silva, C. and Valls, C.. Nonuniform behavior and robustness. J. Differ. Equ. 246 (2009), 3579–3608.Google Scholar
Barreira, L. and Valls, C.. Stable manifolds for nonautonomous equations without exponential dichotomy. J. Differ. Equ. 221 (2006), 58–90.Google Scholar
Barreira, L. and Valls, C.. Robustness of nonuniform exponential dichotomies in Banach spaces. J. Differ. Equ. 244 (2008), 2407–2447.Google Scholar
Chicone, C. and Latushkin, Yu.. Evolution semigroups in dynamical systems and differential equations. Mathematical Surveys and Monographs, vol. 70 (American Mathematical Society, 1999). http://www.ams.org/books/surv/070/Google Scholar
Chow, S. N. and Leiva, H.. Dynamical spectrum for time dependent linear systems in Banach spaces. Jpn. J. Ind. Appl. Math. 11 (1994), 379–415.Google Scholar
Chow, S. N. and Leiva, H.. Existence and roughness of the exponential dichotomy for skew-product semiflows in Banach spaces. J. Differ. Equ. 120 (1995), 429–477.Google Scholar
Coffman, C. V. and Schäffer, J. J.. Linear differential equations with delays: admissibility and conditional exponential stability. J. Differ. Equ. 9 (1971), 521–535.Google Scholar
Coppel, W. A.. Dichotomy in stability theory. Lecture Notes in Mathematics, vol. 629 (New York/Berlin: Springer-Verlag, 1978).Google Scholar
Dalec'kiĭ, J. L. and Kreĭn, M. G.. Stability of differential equations in Banach space (Providence, R.I.: American Mathematical Society, 1974).Google Scholar
Doan, T. S., Rasmussen, M. and Kloeden, P. E.. The mean-square dichotomy spectrum and a bifurcation to a mean-square attractor. Discrete Contin. Dyn. Syst. Ser. B 20 (2015), 875–887.Google Scholar
Engel, K. J. and Nagel, R.. One-parameter semigroups for linear evolution equations (Springer-Verlag, 2000). https://link.springer.com/book/10.1007/b97696Google Scholar
Evans, L. C.. An introduction to stochastic differential equations (American Mathematical Society, 2013). http://www.ams.org/books/mbk/082/Google Scholar
Fu, M. and Liu, Z.. Square-mean almost automorphic solutions for some stochastic differential equations. Proc. Amer. Math. Soc. 138 (2010), 3689–3701.Google Scholar
Hale, J. K.. Ordinary differential equations (New York: Wiley-Interscience, 1969).Google Scholar
Hale, J. and Lin, X. B.. Heteroclinic orbits for retarded functional differential equations. J. Differ. Equ. 65 (1986), 175–202.Google Scholar
Henry, D.. Geometric theory of semilinear parabolic equations. Lecture Notes in Math, vol. 840 (Berlin: Springer-Verlag, 1981).Google Scholar
Higham, D. J.. Mean-square and asymptotic stability of the stochastic theta method. SIAM J. Num. Anal. 38 (2000), 753–769.Google Scholar
Higham, D. J., Mao, X. and Stuart, A. M.. Exponential mean-square stability of numerical solutions to stochastic differential equations. LMS J. Comput. Math. 6 (2003), 297–313.Google Scholar
Higham, D. J., Mao, X. and Yuan, C. G.. Preserving exponential mean-square stability in the simulation of hybrid stochastic differential equations. Numer. Math. 108 (2007), 295–325.Google Scholar
Huy, N. T.. Exponential dichotomy of evolution equations and admissibility of function spaces on a half-line. J. Funct. Anal. 235 (2006), 330–354.CrossRefGoogle Scholar
Imkeller, P. and Lederer, C.. On the cohomology of flows of stochastic and random differential equations. Prob. Theory Related Fields 120 (2001), 209–235.CrossRefGoogle Scholar
Ju, N. and Wiggins, S.. On roughness of exponential dichotomy. J. Math. Anal. Appl. 262 (2001), 39–49.Google Scholar
Kloeden, P. E. and Lorenz, T.. Mean-square random dynamical systems. J. Differ. Equ. 253 (2012), 1422–1438.Google Scholar
Ladde, A. G. and Ladde, G. S.. An introduction to differential equations. Stochastic Modeling, Methods and Analysis, vol. 2 (World Scientific Publishing Co, 2013). https://www.worldscientific.com/worldscibooks/10.1142/8384#t=aboutBookGoogle Scholar
Latushkin, Y., Montgomery-Smith, S. and Randolph, T.. Evolutionary semigroups and dichotomy of linear skew-product flows on locally compact spaces with Banach fibers. J. Differ. Equ. 125 (1996), 73–116.Google Scholar
Latushkin, Y., Randolph, T. and Schnaubelt, R.. Exponential dichotomy and mild solutions of nonautonomous equations in Banach spaces. J. Dynam. Differ. Equ. 10 (1998), 489–510.Google Scholar
Lin, X. B.. Exponential dichotomies and homoclinic orbits in functional differential equations. J. Differ. Equ. 63 (1986), 227–254.Google Scholar
Lin, X. B.. Exponential dichotomies in intermediate spaces with applications to a diffusively perturbed predator-prey model. J. Differ. Equ. 108 (1994), 36–63.Google Scholar
Liu, Z. and Sun, K.. Almost automorphic solutions for stochastic differential equations driven by Lévy noise. J. Funct. Anal. 226 (2014), 1115–1149.Google Scholar
Lizana, M.. Exponential dichotomy for singularly perturbed linear functional differential equation with small delays. Appl. Anal. 47 (1992), 213–225.Google Scholar
Mao, X.. Stochastic differential equations and applications (Chichester: Horwood, 1997).Google Scholar
Massera, J. and Schäffer, J.. Linear differential equations and functional analysis I. Ann. Math. 67 (1958), 517–573.Google Scholar
Naulin, R. and Pinto, M.. Roughness of $(h,\,k)$-dichotomies. J. Differ. Equ. 118 (1995), 20–35.Google Scholar
Naulin, R. and Pinto, M.. Stability of discrete dichotomies for linear difference systems. J. Differ. Equ. Appl. 3 (1997), 101–123.Google Scholar
Palmer, K. J.. Exponential dichotomies and transversal homoclinic points. J. Differ. Equ. 55 (1984), 225–256.Google Scholar
Palmer, K. J.. Exponential dichotomies and Fredholm operators. Proc. Amer. Math. Soc. 104 (1988), 149–156.Google Scholar
Perron, O.. Die Stabilitätsfrage bei Differentialgleichungen. Math. Z. 32 (1930), 703–728.Google Scholar
Pecelli, G.. Dichotomies for linear functional-differential equations. J. Differ. Equ. 9 (1971), 555–579.Google Scholar
Pliss, V. and Sell, G.. Robustness of exponential dichotomies in infinite-dimensional dynamical systems. J. Dynam. Differ. Equ. 11 (1999), 471–513.Google Scholar
Popescu, L. H.. Exponential dichotomy roughness on Banach spaces. J. Math. Anal. Appl. 314 (2006), 436–454.Google Scholar
Popescu, L. H.. Exponential dichotomy roughness and structural stability for evolution families without bounded growth and decay. Nonlinear Anal., 71 (2009), 935–947.Google Scholar
Preda, P., Pogan, A. and Preda, C.. On $(a,\,b)$-dichotomy for evolutionary processes on a half-line. Glasg. Math. J. 46 (2004), 217–225.Google Scholar
Preda, P., Pogan, A. and Preda, C.. Schäffer spaces and exponential dichotomy for evolutionary processes. J. Differ. Equ. 230 (2006), 378–391.Google Scholar
Rodrigues, H. M. and Ruas-Filho, J. G.. Evolution equations dichotomies and the Fredholm alternative for bounded solutions. J. Differ. Equ. 119 (1995), 263–283.Google Scholar
Sacker, R. and Sell, G.. Dichotomies for linear evolutionary equations in Banach spaces. J. Differ. Equ. 113 (1994), 17–67.Google Scholar
Sacker, R. and Sell, G.. Existence of dichotomies and invariant splitting for linear differential systems I [II, III]. J. Differ. Equ. 15 (1974), 429–458.Google Scholar
Stanzhyts'kyi, O. M.. Exponential dichotomy and mean square bounded solutions of linear stochastic Ito systems. Nonlinear Oscil. 4 (2001), 389–398.Google Scholar
Stanzhyts'kyi, O. M. and Krenevych, A. P.. Investigation of the exponential dichotomy of linear stochastic Itô systems with random initial data by means of quadratic forms. Ukrainian Math. J. 58 (2006), 619–629.Google Scholar
Stoica, D.. Uniform exponential dichotomy of stochastic cocycles. Stochastic Process. Appl. 120 (2010), 1920–1928.Google Scholar
Zhou, L., Lu, K. and Zhang, W.. Roughness of tempered exponential dichotomies for infinite-dimensional random difference equations. J. Differ. Equ. 254 (2013), 4024–4046.CrossRefGoogle Scholar
Zhou, L., Lu, K. and Zhang, W.. Equivalences between nonuniform exponential dichotomy and admissibility. J. Differ. Equ. 262 (2017), 682–747.Google Scholar
Zhou, L. and Zhang, W.. Admissibility and roughness of nonuniform exponential dichotomies for difference equations. J. Funct. Anal. 271 (2016), 1087–1129.Google Scholar
Zhu, H. and Chu, J.. Mean-square exponential dichotomy of numerical solutions to stochastic differential equations. J. Appl. Anal. Comput. 6 (2016), 463–478.Google Scholar
Zhu, H. and Jiang, Y.. Robustness of mean-square exponential dichotomies for linear stochastic equations. Electron. J. Differ. Equ. 123 (2017), 1–13.Google Scholar
Zhu, H., Chu, J. and Zhang, W.. Mean-square Almost automorphic solutions for stochastic differential equations with hyperbolicity. Discrete Contin. Dyn. Syst. 38 (2018), 1935–1953.Google Scholar
Zhu, H. and Chen, L.. Nonuniform exponential dichotomies in mean square and second-moment Lyapunov exponent. Nonlinear Anal. 196 (2020), 111806.Google Scholar