Article contents
Radial entire solutions to even order semilinear elliptic equations in the plane
Published online by Cambridge University Press: 14 November 2011
Synopsis
Semilinear elliptic equations of the form
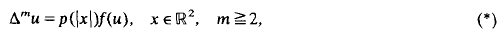
are considered, where Δm is the m-th iterate of the two-dimensional Laplacian Δ, p(t) is continuous in [0, ∞), and f(u is continuous and positive either in (0, ∞) or in ℝ.
Our main objective is to present conditions on p and f which imply the existence of radial entire solutions to (*), that is, those functions of class C2m(ℝ2) which depend only on |x| and satisfy (*) pointwise in ℝ2.
First, necessary and sufficient conditions are established for equation (*), with p(t) > 0 in [0, ∞), to possess infinitely many positive radial entire solutions which are asymptotic to positive constant multiples of |x|2m−2 log |x as |x| → ∞. Secondly, it is shown that, in the case p(t < 0, in [ 0, ∞) and f(u) > 0 is nondecreasing in ℝ, equation (*) always has eventually negative radial entire solutions, all of which decrease at least as fast as negative constant multiples of |x|2m−2 log |x| as |x| → ∞. Our results seem to be new even when specialised to the prototypes
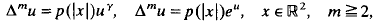
where γ is a constant.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 105 , Issue 1 , 1987 , pp. 275 - 287
- Copyright
- Copyright © Royal Society of Edinburgh 1987
References
- 8
- Cited by


