Article contents
On the completeness of eigenvectors of right definite multiparameter problems
Published online by Cambridge University Press: 14 November 2011
Synopsis
We prove that there exists a complete system of eigenvectors of the eigenvalue problem
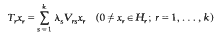
for self-adjoint operators Tr and Vrs on separable Hilbert spaces Hr. It is assumed that
(i) the operators Tr have discrete spectrum;
(ii) the operators Vrs are bounded and commute for each r;
(iii) the operators Vrs have the definite sign factor property.
This theorem generalizes and improves a result of Cordes for two-parameter problems. The proof of the theorem depends on an approximation of the given eigenvalue problem by simpler problems, a technique which is related to Atkinson's proof of his expansion theorem.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 96 , Issue 1-2 , 1984 , pp. 69 - 78
- Copyright
- Copyright © Royal Society of Edinburgh 1984
References
- 6
- Cited by


