Hostname: page-component-6bf8c574d5-gr6zb Total loading time: 0 Render date: 2025-02-25T16:52:16.220Z Has data issue: false hasContentIssue false
  • English
  • Français

On structure theory of pre-Hilbert algebras

Published online by Cambridge University Press:  25 March 2009

José Antonio Cuenca Mira
José Antonio Cuenca Mira
Affiliation:
Departamento de Àlgebra, Geometría y Topología, Facultad de Ciencias, Universidad de Málaga, 29080 Málaga, Spain ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let A be a real (non-associative) algebra which is normed as real vector space, with a norm ‖·‖ deriving from an inner product and satisfying ‖ac‖ ≤ ‖a‖‖c‖ for any a,c ∈ A. We prove that if the algebraic identity (a((ac)a))a = (a2c)a2 holds in A, then the existence of an idempotent e such that ‖e‖ = 1 and ‖ea‖ = ‖a‖ = ‖ae‖, a ∈ A, implies that A is isometrically isomorphic to ℝ, ℂ, ℍ, 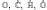or ℙ. This is a non-associative extension of a classical theorem by Ingelstam. Finally, we give some applications of our main result.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 139 , Issue 2 , April 2009 , pp. 303 - 319
Copyright
Copyright © Royal Society of Edinburgh 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)