Article contents
On multiple solutions for Berman's problem
Published online by Cambridge University Press: 14 November 2011
Synopsis
We study Berman's problem
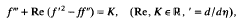
subjects to the conditions f(0) =f″(0) = f′(1) = f(1)− 1 = 0, which arises from the study of laminar flows in channels with porous walls. Positive (negative) Re denotes the case of suction (injection) flows. Preliminary numerical studies indicated the existence of three different types of solutions and a small portion of mathematical evidence was provided. In this paper, we are able to show that there exist connected sets in the Re-K plane on which different types of solutions occur. In particular, our result verifies that the problem possesses all three types of suction solutions for sufficiently large Re. Moreover, the limiting injection solution is also obtained.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 121 , Issue 3-4 , 1992 , pp. 219 - 230
- Copyright
- Copyright © Royal Society of Edinburgh 1992
References
- 6
- Cited by


