Hostname: page-component-f554764f5-fnl2l Total loading time: 0 Render date: 2025-04-21T08:21:59.990Z Has data issue: false hasContentIssue false
  • English
  • Français

On generalized eigenvalue problems of fractional (p, q)-Laplace operator with two parameters

Part of: Integral, integro-differential, and pseudodifferential operators Elliptic equations and systems Partial differential equations Spectral theory and eigenvalue problems

Published online by Cambridge University Press:  22 January 2024

Nirjan Biswas Open the ORCID record for Nirjan Biswas [Opens in a new window]  and
Firoj Sk Open the ORCID record for Firoj Sk [Opens in a new window]
Nirjan Biswas
Affiliation:
Tata Institute of Fundamental Research, Centre For Applicable Mathematics, Post Bag No 6503, Sharada Nagar, Bangalore 560065, India ([email protected])
Firoj Sk
Affiliation:
Carl von Ossietzky Universität Oldenburg, Fakultät V, Institut für Mathematik, Ammerländer Heerstraße 114–118, 26129 Oldenburg, Germany ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

For $s_1,\,s_2\in (0,\,1)$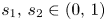 and $p,\,q \in (1,\, \infty )$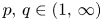, we study the following nonlinear Dirichlet eigenvalue problem with parameters $\alpha,\, \beta \in \mathbb {R}$ 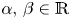driven by the sum of two nonlocal operators: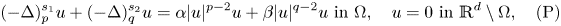

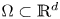\[ (-\Delta)^{s_1}_p u+(-\Delta)^{s_2}_q u=\alpha|u|^{p-2}u+\beta|u|^{q-2}u\ \text{in }\Omega, \quad u=0\ \text{in } \mathbb{R}^d \setminus \Omega, \quad \mathrm{(P)} \]
where $\Omega \subset \mathbb {R}^d$ is a bounded open set. Depending on the values of $\alpha,\,\beta$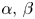, we completely describe the existence and non-existence of positive solutions to (P). We construct a continuous threshold curve in the two-dimensional $(\alpha,\, \beta )$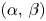-plane, which separates the regions of the existence and non-existence of positive solutions. In addition, we prove that the first Dirichlet eigenfunctions of the fractional $p$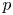-Laplace and fractional $q$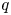-Laplace operators are linearly independent, which plays an essential role in the formation of the curve. Furthermore, we establish that every nonnegative solution of (P) is globally bounded.

Keywords

Generalized eigenvalue problemsfractional (p, q)-Laplace operatorpositive solutionNehari manifoldlinear independence of the eigenfunctions

MSC classification

Primary: 35A01: Existence problems
Secondary: 35B09: Positive solutions 35B38: Critical points 35J60: Nonlinear elliptic equations 35P30: Nonlinear eigenvalue problems, nonlinear spectral theory 47G20: Integro-differential operators
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 46
Check for updates
Copyright
Copyright © The Author(s), 2024. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

This article has been updated since it was orignially published. A notice detailing this has been published and the errors rectified in the online PDF and HTML copies.

References

Ambrosetti, A. and Rabinowitz, P. H.. Dual variational methods in critical point theory and applications. J. Funct. Anal. 14 (1973), 349–381. doi:10.1016/0022-1236(73)90051-7CrossRefGoogle Scholar
Ambrosio, V.. Fractional $(p,\,q)$ Laplacian problems in $\mathbb {R}^N$ with critical growth. Z. Anal. Anwend. 39 (2020), 289–314. doi:10.4171/zaa/1661CrossRefGoogle Scholar
Ambrosio, V.. A strong maximum principle for the fractional $(p,\,q)$-Laplacian operator. Appl. Math. Lett. 126 (2022), 107813. doi:10.1016/j.aml.2021.107813CrossRefGoogle Scholar
Ambrosio, V. and Isernia, T.. Multiplicity of positive solutions for a fractional $p\& q$-Laplacian problem in $\Bbb R^N$. J. Math. Anal. Appl. 501 (2021), 124487. doi:10.1016/j.jmaa.2020.124487CrossRefGoogle Scholar
Antil, H. and Warma, M.. Optimal control of the coefficient for the regional fractional $p$-Laplace equation: approximation and convergence. Math. Control Relat. Fields 9 (2019), 1–38. doi:10.3934/mcrf.2019001CrossRefGoogle Scholar
Bai, Y., Papageorgiou, N. S. and Zeng, S.. A singular eigenvalue problem for the Dirichlet $(p,\,q)$-Laplacian. Math. Z. 300 (2022), 325–345. doi:10.1007/s00209-021-02803-wCrossRefGoogle Scholar
Bhakta, M. and Mukherjee, D.. Multiplicity results for $(p,\,q)$ fractional elliptic equations involving critical nonlinearities. Adv. Differ. Equ. 24 (2019), 185–228. https://projecteuclid.org/euclid.ade/1548212469Google Scholar
Bobkov, V. and Tanaka, M.. On positive solutions for $(p,\,q)$-Laplace equations with two parameters. Calc. Var. Partial Differ. Equ. 54 (2015), 3277–3301. doi:10.1007/s00526-015-0903-5CrossRefGoogle Scholar
Bobkov, V. and Tanaka, M.. Remarks on minimizers for $(p,\,q)$-Laplace equations with two parameters. Commun. Pure Appl. Anal. 17 (2018), 1219–1253. doi:10.3934/cpaa.2018059CrossRefGoogle Scholar
Bobkov, V. and Tanaka, M.. Generalized Picone inequalities and their applications to ($p$,$q$)-Laplace equations. Open Math. 18 (2020), 1030–1044. doi:10.1515/math-2020-0065CrossRefGoogle Scholar
Brasco, L. and Franzina, G.. Convexity properties of Dirichlet integrals and Picone-type inequalities. Kodai Math. J. 37 (2014), 769–799. doi:10.2996/kmj/1414674621CrossRefGoogle Scholar
Brasco, L., Lindgren, E. and Parini, E.. The fractional Cheeger problem. Interfaces Free Bound. 16 (2014), 419–458. doi:10.4171/IFB/325CrossRefGoogle Scholar
Brasco, L., Lindgren, E. and Schikorra, A.. Higher Hölder regularity for the fractional $p$-Laplacian in the superquadratic case. Adv. Math. 338 (2018), 782–846. doi:10.1016/j.aim.2018.09.009CrossRefGoogle Scholar
Brasco, L. and Parini, E.. The second eigenvalue of the fractional $p$-Laplacian. Adv. Calc. Var. 9 (2016), 323–355. doi:10.1515/acv-2015-0007CrossRefGoogle Scholar
Cherfils, L. and Il'yasov, Y.. On the stationary solutions of generalized reaction diffusion equations with $p\, \& \,q$-Laplacian. Commun. Pure Appl. Anal. 4 (2005), 9–22.CrossRefGoogle Scholar
Del P., L. M. and Quaas, A.. Global bifurcation for fractional $p$-Laplacian and an application. Z. Anal. Anwend. 35 (2016), 411–447. doi:10.4171/ZAA/1572CrossRefGoogle Scholar
Del P., Leandro M. and Quaas, A.. A Hopf's lemma and a strong minimum principle for the fractional $p$-Laplacian. J. Differ. Equ. 263 (2017), 765–778. doi:10.1016/j.jde.2017.02.051CrossRefGoogle Scholar
Derrick, G. H.. Comments on nonlinear wave equations as models for elementary particles. J. Math. Phys. 5 (1964), 1252–1254. doi:10.1063/1.1704233CrossRefGoogle Scholar
Di Nezza, E., Palatucci, G. and Valdinoci, E.. Hitchhiker's guide to the fractional Sobolev spaces. Bull. Sci. Math. 136 (2012), 521–573. doi:10.1016/j.bulsci.2011.12.004CrossRefGoogle Scholar
Fife, P. C., Mathematical aspects of reacting and diffusing systems, Lecture Notes in Biomathematics, Vol. 28 (Springer-Verlag, Berlin-New York, 1979).CrossRefGoogle Scholar
Franzina, G. and Palatucci, G.. Fractional $p$-eigenvalues. Riv. Math. Univ. Parma (N.S.) 5 (2014), 373–386.Google Scholar
Garain, P. and Lindgren, E., Higher Hölder regularity for the fractional $p$-Laplacian equation in the subquadratic case. arXiv:2310.03600 (2023).Google Scholar
Giacomoni, J., Gouasmia, A. and Mokrane, A.. Discrete Picone inequalities and applications to non local and non homogenenous operators. Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Mat. RACSAM 116 (2022), 100. doi:10.1007/s13398-022-01241-5CrossRefGoogle Scholar
Giacomoni, J., Kumar, D. and Sreenadh, K.. Global regularity results for non-homogeneous growth fractional problems. J. Geom. Anal. 32 (2022), 36. doi:10.1007/s12220-021-00837-4CrossRefGoogle Scholar
Goel, D., Kumar, D. and Sreenadh, K.. Regularity and multiplicity results for fractional $(p,\,q)$-Laplacian equations. Commun. Contemp. Math. 22 (2020), 1950065. doi:10.1142/S0219199719500652CrossRefGoogle Scholar
Goyal, S. and Sreenadh, K.. On the Fučik spectrum of non-local elliptic operators. NoDEA Nonlinear Differ. Equ. Appl. 21 (2014), 567–588. doi:10.1007/s00030-013-0258-6CrossRefGoogle Scholar
Iannizzotto, A., Mosconi, S. and Squassina, M.. Global Hölder regularity for the fractional $p$-Laplacian. Rev. Mat. Iberoam. 32 (2016), 1353–1392. doi:10.4171/RMI/921CrossRefGoogle Scholar
Iannizzotto, A., Mosconi, S. and Squassina, M.. Sobolev versus Hölder minimizers for the degenerate fractional $p$-Laplacian. Nonlinear Anal. 191 (2020), 111635. doi:10.1016/j.na.2019.111635CrossRefGoogle Scholar
Motreanu, D. and Tanaka, M.. On a positive solution for $(p,\,q)$-Laplace equation with indefinite weight. Minimax Theory Appl. 1 (2016), 1–20.Google Scholar
Nguyen, T. H. and Vo, H. H., Principal eigenvalue and positive solutions for fractional $p-q$ laplace operator in quantum field theory. preprint arXiv:2006.03233 (2020).Google Scholar
Perera, K., Squassina, M. and Yang, Y.. A note on the Dancer–Fučík spectra of the fractional $p$-Laplacian and Laplacian operators. Adv. Nonlinear Anal. 4 (2015), 13–23. doi:10.1515/anona-2014-0038CrossRefGoogle Scholar
T. Kuusi, Agnese D. C. and Palatucci, G.. Nonlocal Harnack inequalities. J. Funct. Anal. 267 (2014), 1807–1836. doi:10.1016/j.jfa.2014.05.023Google Scholar
Tanaka, M.. Generalized eigenvalue problems for $(p,\,q)$-Laplacian with indefinite weight. J. Math. Anal. Appl. 419 (2014), 1181–1192. doi:10.1016/j.jmaa.2014.05.044CrossRefGoogle Scholar