Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-27T20:55:37.842Z Has data issue: false hasContentIssue false
  • English
  • Français

On a family of torsional creep problems involving rapidly growing operators in divergence form

Published online by Cambridge University Press:  26 December 2018

Maria Fărcăşeanu  and
Mihai Mihăilescu
Maria Fărcăşeanu
Affiliation:
Department of Mathematics, University of Craiova, Craiova 200585, Romania
Mihai Mihăilescu
Affiliation:
Research group of the project PN-III-P4-ID-PCE-2016-0035, ‘Simion Stoilow’Institute of Mathematics of the Romanian Academy, Bucharest 010702, Romania ([email protected]; [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let Ω⊂ℝN (N≥2) be a bounded domain with smooth boundary and {pn} be a sequence of real numbers converging to+∞ as n→∞. For each integer n>1, we define the function 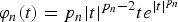$\varphi_{n}(t)=p_{n} \vert t \vert^{p_{n}-2}te^{ \vert t \vert^{p_{n}}}$, for all t∈ℝ, and we prove the existence of a unique nonnegative variational solution for the problem−div(((φn(|∇ u(x)|))/(|∇ u(x)|))∇ u(x))=φn(1), when x∈Ω, subject to the homogeneous Dirichlet boundary condition. Next, we establish the uniform convergence in Ω of the sequence of solutions for the above family of equations to the distance function to the boundary of Ω. Our result complements the earlier developments on the topic obtained by Payne and Philippin [26], Kawohl [21], Bhattacharya, DiBenedetto and Manfredi [2], Perez-Llanos and Rossi [27] and Bocea and Mihăilescu [4].

Keywords

rapidly growing differential operatorOrlicz-Sobolev spacevariational solutionΓ-convergencedistance function to the boundaryPrimary: 35D3035J92Secondary: 46E3049J4049J45
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 149 , Issue 2 , April 2019 , pp. 495 - 510
Copyright
Copyright © Royal Society of Edinburgh 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Adams, R.. Sobolev Spaces. (New York: Academic Press, 1975).Google Scholar
2Bhattacharya, T., DiBenedetto, E. and Manfredi, J.. Limits as p→∞ of Δ pu p = f and related extremal problems. Rend. Sem. Mat. Univ. Politec. Torino special issue (1991), 15–68.Google Scholar
3Bocea, M. and Mihăilescu, M.. Eigenvalue problems in Orlicz-Sobolev spaces for rapidly growing operators in divergence form. J. Differential Equations 256 (2014), 640–657.Google Scholar
4Bocea, M. and Mihăilescu, M.. On a family of inhomogeneous torsional creep problems. Proc. Amer. Math. Soc. 145 (2017), 4397–4409.Google Scholar
5Braides, A.. G-convergence for beginners. Oxford Lecture Series in Mathematics and its Applications, 22 (Oxford University Press, 2002).Google Scholar
6Clément, P., de Pagter, B., Sweers, G. and de Télin, F.. Existence of solutions to a semilinear elliptic system through Orlicz-Sobolev spaces. Mediterr. J. Math. 1 (2004), 3, 241–267.Google Scholar
7Dal Maso, G.. An introduction to Γ-convergence. Progress in nonlinear differential equations and their applications, vol. 8 (Boston, MA: Birkäuser, 1993).Google Scholar
8De Giorgi, E.. Sulla convergenza di alcune succesioni di integrali del tipo dell'area. Rend. Mat. 8 (1975), 277–294.Google Scholar
9De Giorgi, E. and Franzoni, T.. Su un tipo di convergenza variazionale. Atti Accad. Naz. Lincei Rend. Cl. Sci. Fis. Mat. Natur. 58 (1975), 842–850.Google Scholar
10Donaldson, T.. Nonlinear elliptic boundary value problems in Orlicz- Sobolev spaces. J. Diff. Equations 10 (1971), 507–528.Google Scholar
11Fukagai, N., Ito, M. and Narukawa, K.. Positive solutions of quasilinear elliptic equations with critical Orlicz-Sobolev nonlinearity on ℝN. Funkcial. Ekvac. 49 (2006), 235–267.Google Scholar
12García-Huidobro, M., Le, V. K., Manásevich, R. and Schmitt, K.. On principal eigenvalues for quasilinear elliptic differential operators: an Orlicz-Sobolev space setting. Nonlinear Differential Equations Appl. (NoDEA) 6 (1999), 207–225.Google Scholar
13Gossez, J. P.. Nonlinear elliptic boundary value problems for equations with rapidly (or slowly) increasing coefficients. Trans. Amer. Math. Soc. 190 (1974), 163–205.Google Scholar
14Gossez, J. P.. A strongly nonlinear elliptic problem in Orlicz-Sobolev spaces. Proc. Symp. Pure Mathematics 45 (1986), 455–462.Google Scholar
15Jensen, R.. Uniqueness of Lipschitz extensions: Minimizing the up norm of the gradient. Arch. Rational Mech. Anal. 123 (1993), 51–74.Google Scholar
16Jost, J. and Li-Jost, X.. Calculus of Variations. Cambridge Studies in Advanced Mathematics, 64. (Cambridge University Press, 2008).Google Scholar
17Juutinen, P.. Minimization problems for Lipschitz functions via viscosity solutions, Thesis University of Jyvaskyla (1996), pp. 1–39.Google Scholar
18Juutinen, P., Lindqvist, P. and Manfredi, J. J.. The ∞-eigenvalue problem. Arch. Rational Mech. Anal. 148 (1999), 89–105.Google Scholar
19Kachanov, L. M.. The theory of creep. Nat. Lending Lib. for Science and Technology, (Yorkshire, England: Boston Spa, 1967).Google Scholar
20Kachanov, L. M.. Foundations of the theory of plasticity. (Amsterdam-London: North-Holland Publishing Co., 1971).Google Scholar
21Kawohl, B.. On a family of torsional creep problems. J. Reine Angew. Math. 410 (1990), 1–22.Google Scholar
22Krasnosels'kii, M. and Rutic'kii, J.. Convex Functions and Orlicz Spaces. (Groningen: Noordhoff, 1961).Google Scholar
23Le, V. K. and Schmitt, K.. Quasilinear elliptic equations and inequalities with rapidly growing coefficients. J. London Math. Soc. 62 (2000), 852–872.Google Scholar
24Lieberman, G. M.. On the regularity of the minimizer of a functional with exponential growth. Comment. Math. Univ. Carolinae 33 (1992), 45–49.Google Scholar
25Lindqvist, P.. On the equation ${\rm div}( \vert \nabla u \vert^{p}-2\nabla u)+\lambda \vert u \vert^{p}-2u=0$. Proc. Amer. Math. Soc 109 (1990), 157–164.Google Scholar
26Payne, L. E. and Philippin, G. A.. Some applications of the maximum principle in the problem of torsional creep. SIAM J. Appl. Math. 33 (1977), 446–455.Google Scholar
27Pérez-Llanos, M. and Rossi, J.D.. The limits as p(x) → ∞ of solutions to the inhomogeneous Dirichlet problem of the p(x)-Laplacian. Nonlinear Analysis 73 (2010), 2027–2035.Google Scholar
28Rao, M. M. and Ren, Z. D.. Theory of Orlicz Spaces. (New York: Marcel Dekker, Inc., 1991).Google Scholar
29Szulkin, A.. Minimax principles for lower semicontinuous functions and applications to nonlinear boundary value problems. Ann. Inst. H. Poincaré Anal. Non Linéaire 3 (1986), 77–109.Google Scholar