Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-28T00:39:03.193Z Has data issue: false hasContentIssue false
  • English
  • Français

Mappings of Lp-integrable distortion: regularity of the inverse

Part of: Functions of several variables Classical measure theory Geometric function theory

Published online by Cambridge University Press:  16 May 2016

Jani Onninen  and
Ville Tengvall
Jani Onninen
Affiliation:
Department of Mathematics and Statistics, University of Jyväskylä, PO Box 35 (MaD), 40014University of Jyväskylä, Finland ([email protected]; [email protected])
Ville Tengvall
Affiliation:
Department of Mathematics and Statistics, University of Jyväskylä, PO Box 35 (MaD), 40014University of Jyväskylä, Finland ([email protected]; [email protected])
Get access Rights & Permissions [Opens in a new window]

Extract

Let 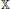be an open set in ℝn and suppose that 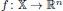is a Sobolev homeomorphism. We study the regularity of f–1 under the Lp-integrability assumption on the distortion function Kf. First, if 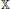is the unit ball and p > n – 1, then the optimal local modulus of continuity of f–1 is attained by a radially symmetric mapping. We show that this is not the case when p ⩽ n – 1 and n ⩾ 3, and answer a question raised by S. Hencl and P. Koskela. Second, we obtain the optimal integrability results for ∣Df–1∣ in terms of the Lp-integrability assumptions of Kf.

Keywords

mappings of finite distortionregularity of the inversemodulus of continuityhigher integrabilitySobolev homeomorphism

MSC classification

Secondary: 30C65: Quasiconformal mappings in $^n$, other generalizations 28A78: Hausdorff and packing measures 26B10: Implicit function theorems, Jacobians, transformations with several variables
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 146 , Issue 3 , June 2016 , pp. 647 - 663
Copyright
Copyright © Royal Society of Edinburgh 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)