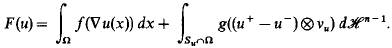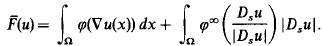Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Braides, Andrea
Defranceschi, Anneliese
and
Vitali, Enrico
1996.
Homogenization of free discontinuity problems.
Archive for Rational Mechanics and Analysis,
Vol. 135,
Issue. 4,
p.
297.
Barroso, Ana Cristina
Bouchitté, Guy
Buttazzo, Giuseppe
and
Fonseca, Irene
1996.
Relaxation of bulk and interfacial energies.
Archive for Rational Mechanics and Analysis,
Vol. 135,
Issue. 2,
p.
107.
Braides, A.
Defranceschi, A.
and
Vitali, E.
1997.
A relaxation approach to hencky’s plasticity.
Applied Mathematics & Optimization,
Vol. 35,
Issue. 1,
p.
45.
Cortesani, Guido
and
Toader, Rodica
1999.
Nonlocal Approximation of Nonisotropic Free-Discontinuity Problems.
SIAM Journal on Applied Mathematics,
Vol. 59,
Issue. 4,
p.
1507.
Fonseca, Irene
and
Malý, Jan
2002.
Applied Nonlinear Analysis.
p.
117.
Bouchitté, Guy
Fonseca, Irene
and
Mascarenhas, Luı́sa
2002.
Relaxation of variational problems under trace constraints.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 49,
Issue. 2,
p.
221.
Ball, John M.
2002.
Geometry, Mechanics, and Dynamics.
p.
3.
Morini, Massimiliano
2003.
Sequences of Singularly Perturbed Functionals Generating Free-Discontinuity Problems.
SIAM Journal on Mathematical Analysis,
Vol. 35,
Issue. 3,
p.
759.
Braides, Andrea
and
Truskinovsky, Lev
2008.
Asymptotic expansions by Γ-convergence.
Continuum Mechanics and Thermodynamics,
Vol. 20,
Issue. 1,
p.
21.
Fonseca, Irene
2008.
Classical and Advanced Theories of Thin Structures.
Vol. 503,
Issue. ,
p.
187.
Fraternali, Fernando
Negri, Matteo
and
Ortiz, Michael
2010.
On the convergence of 3D free discontinuity models in variational fracture.
International Journal of Fracture,
Vol. 166,
Issue. 1-2,
p.
3.
Fraternali, Fernando
Negri, Matteo
and
Ortiz, Michael
2010.
Recent Progress in the Mechanics of Defects.
p.
3.
Soneji, Parth
2014.
Relaxation in BV of integrals with superlinear growth.
ESAIM: Control, Optimisation and Calculus of Variations,
Vol. 20,
Issue. 4,
p.
1078.
Kristensen, Jan
and
Rindler, Filip
2016.
Piecewise affine approximations for functions of bounded variation.
Numerische Mathematik,
Vol. 132,
Issue. 2,
p.
329.
Braides, Andrea
and
Nodargi, Nicola A
2020.
Homogenization of cohesive fracture in masonry structures.
Mathematics and Mechanics of Solids,
Vol. 25,
Issue. 2,
p.
181.
Conti, Sergio
Focardi, Matteo
and
Iurlano, Flaviana
2024.
Phase-Field Approximation of a Vectorial, Geometrically Nonlinear Cohesive Fracture Energy.
Archive for Rational Mechanics and Analysis,
Vol. 248,
Issue. 2,
Conti, Sergio
Focardi, Matteo
and
Iurlano, Flaviana
2025.
Approximation of SBV functions with possibly infinite jump set.
Journal of Functional Analysis,
Vol. 288,
Issue. 2,
p.
110686.