Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-01-12T19:09:58.301Z Has data issue: false hasContentIssue false
  • English
  • Français

Geršgorin theory and the definiteness of determinantal operators

Published online by Cambridge University Press:  14 November 2011

D. R. Farenick  and
Patrick J. Browne
D. R. Farenick
Affiliation:
Department of Mathematics and Statistics, University of Calgary, Calgary, Alberta, CanadaT2N 1N4
Patrick J. Browne
Affiliation:
Department of Mathematics and Statistics, University of Calgary, Calgary, Alberta, CanadaT2N 1N4
Get access Rights & Permissions [Opens in a new window]

Synopsis

Let Aij, l≦j≦k, be bounded Hermitean operators on Hilbert spaces Hi, 1≦i≦k, and let 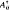be the induced operators on 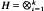. An important operator for multiparameter theory is δ: H →H denned by δ = det 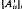the determinant being expanded formally. Various definiteness properties of δ are critical for multiparameter spectral theory.

We use the operators Aij to construct a numerical matrix δ(δ) upon which we use Geršgorin theory to investigate the non-singularity and definiteness of δ. Diagonal dominance properties of the array [Aij] are also discussed.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 106 , Issue 1-2 , 1987 , pp. 1 - 10
Copyright
Copyright © Royal Society of Edinburgh 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Atkinson, F. V.. Multiparameter Eigenvalue Problems, Vol. I (New York: Academic Press, 1972).Google Scholar
2Berman, A. and Plemmons, R. J.. Nonnegative Matrices in the Mathematical Sciences (New York: Academic Press, 1979).Google Scholar
3Binding, P.. Another positivity result for determinantal operators. Proc. Roy. Soc. Edinburgh Sect. A 86 (1980), 333–337.CrossRefGoogle Scholar
4Binding, P. and Browne, P. J.. A definiteness result for determinantal operators. Proceedings of the Dundee Symposium on Ordinary Differential Equations and Operators, 1982. Lecture Notes in Mathematics 1032, pp. 17–30 (Berlin: Springer, 1983).Google Scholar
5Brauer, A.. Limits for the characteristic roots of matrices II. Duke Math. J. 14 (1947), 21–26.CrossRefGoogle Scholar
6Farenick, D. R.. Geršgorin Theory and Determinantal Operators (M.Sc. Thesis, University of Calgary, 1986).Google Scholar
7Geršgorin, S.. Über die Abgrenzung der Eigenwerte einer Matrix. Izv. Akad. Nauk SSSR. Otd. Mat. Estetv. Nauk 7 (1931), 749–754.Google Scholar
8Johnson, C. R.. A GerSgorin inclusion set for the field of values of a finite matrix. Proc. Amer. Math. Soc. 41 (1973), 57–60.Google Scholar
9Levinger, B. W.. Minimal Geršgorin sets III. Linear Algebra Appl. 2 (1962), 13–19.CrossRefGoogle Scholar
10Minkowski, H.. Zur Theorie der einheiten in den algebraischen Zahlkörpern. Nachr. K. Ges. Wiss. Gött., Math-Phys. Klasse (1900), 90–93.Google Scholar
11Sleeman, B. D.. Multiparameter Spectral Theory in Hilbert Space (London: Pitman, 1978).CrossRefGoogle Scholar
12Taussky, O.. A recurring theorem on determinants. Amer. Math. Monthly 51 (1949), 672–676.CrossRefGoogle Scholar
13Varga, R. S.. Matrix Iterative Analysis (Englewood Cliffs, New Jersey: Prentice-Hall, 1962).Google Scholar
14Varga, R. S.. Minimal Geršgorin sets. Pacific J. Math. 15 (1965), 719–729.CrossRefGoogle Scholar