Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-23T04:52:56.005Z Has data issue: false hasContentIssue false
  • English
  • Français

Existence results for semilinear problems in the two-dimensional hyperbolic space involving critical growth

Part of: Elliptic equations and systems Partial differential equations on manifolds; differential operators Partial differential equations

Published online by Cambridge University Press:  06 January 2017

Debdip Ganguly  and
Debabrata Karmakar
Debdip Ganguly
Affiliation:
Dipartimento di Scienze Matematiche, Politecnico Di Torino, Corso Duca degli Abruzzi, 24, 10129 Torino, Italy ([email protected])
Debabrata Karmakar
Affiliation:
Centre for Applicable Mathematics, Tata Institute of Fundamental Research, PO Box 6503, GKVK Post Office, Bangalore 560065, India ([email protected])
Get access Rights & Permissions [Opens in a new window]

Extract

We consider semilinear elliptic problems on two-dimensional hyperbolic space. A model problem of our study is

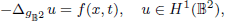
where H 1(𝔹2) denotes the Sobolev space on the disc model of the hyperbolic space and f(x, t) denotes the function of critical growth in dimension 2. We first establish the Palais–Smale (PS) condition for the functional corresponding to the above equation, and using the PS condition we obtain existence of solutions. In addition, using a concentration argument, we also explore existence of infinitely many sign-changing solutions.

Keywords

semilinear elliptic problemhyperbolic spacecritical growthMoser–Trudinger inequality

MSC classification

Secondary: 35J20: Variational methods for second-order elliptic equations 35J60: Nonlinear elliptic equations 35J61: Semilinear elliptic equations 35B33: Critical exponents 58J05: Elliptic equations on manifolds, general theory
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 147 , Issue 1 , February 2017 , pp. 141 - 176
Copyright
Copyright © Royal Society of Edinburgh 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)