Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T17:31:42.279Z Has data issue: false hasContentIssue false
  • English
  • Français

Estimates for the state density for ordinary differential operators with white gaussian noise potential

Published online by Cambridge University Press:  14 November 2011

V. B. Moscatelli  and
M. Thompson
V. B. Moscatelli
Affiliation:
Instituto di Mathematicà, Universita CP 113, Via Arnessano 13100, Lecce, Italia
M. Thompson
Affiliation:
Dept° de Mathemática, U.F.R.G.S. 3° andar, 425 Rua Sarmento Leite, 90.000 - Porto Alegre, Rio Grande do Sul, Brasil
Get access Rights & Permissions [Opens in a new window]

Synopsis

The present paper is concerned with developing the existence and asymptotic properties of the state density N(λ) associated with certain higher order random ordinary differential operators A of the form

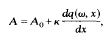
where Ao has homogeneous and ergodic coefficients with respect to the σ-algebra generated by the Wiener process q(ω, x). The analysis uses the Weyl min-max principle to determine rough upper and lower bounds for N(λ).

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 95 , Issue 3-4 , 1983 , pp. 263 - 274
Copyright
Copyright © Royal Society of Edinburgh 1983

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Coddington, E. A. and Levinson, N.. The theory of ordinary differential equations (New York: McGraw-Hill, 1955).Google Scholar
2Doob, J. L.. Stochastic process (New York: John Wiley, 1967).Google Scholar
3Friedman, A.. Stochastic differential equations and applications, Vols I and II (New York: 1975, 1976).Google Scholar
4Frisch, H. L. and Lloyd, S. P.. Electron levels in a one-dimensional random lattice. Phys. Rev. 120 (1960), 1175–1189.CrossRefGoogle Scholar
5Fukushima, M. and Nakao, S.. On the spectra of the Schrodinger operator with White Gaussian Noise potential. Z. Wahrsch. 37 (1977), 267–274.CrossRefGoogle Scholar
6Gihman, I. I. and Skorohod, A. V.. The theory of stochastic process, Vol. II (Berlin: Springer, 1975).Google Scholar
7Gihman, I. I. and Skorohod, A. V.. Stochastic differential equations (Berlin: Springer, 1973).Google Scholar
8Métivier, G.. Valeurs propres de problemes aux limites irregulieres. Bull. Soc. Math. France Mem. 51–52 (1977), 125–219.Google Scholar
9Nakao, S. and Yamoto, Y.. Approximation theorem on stochastic differential equations. Proc. Internat. Symp. Stochastic Differential Equations, Kyoto 1976, 283–296 (New York: Wiley, 1978).Google Scholar
10Parthasarathy, K. K.. Probability measures on metric spaces (London: Academic Press, 1976).Google Scholar
11Pastur, L. A.. Spectra of random self-adjoint operators. Russian Math. Surveys 28 (1973), 1–67.CrossRefGoogle Scholar
12Thompson, M.. The state density of elliptic operators with random potentials. Ann. Mat. Pura Appl. 131 (1982), 29–56.Google Scholar
13Thompson, M.. The state density for second order ordinary differential equations with White Gaussian Noise Potential. IV Congresso Nacional de Matematica Aplicada e Computational R. J., Setembro 1981. Boll. Un. Mat. Ital. 6 2–B (1983), 283–296.Google Scholar