Article contents
Enumeration of smooth labelled graphs
Published online by Cambridge University Press: 14 November 2011
Synopsis
An (n, q) graph is a graph on n labelled points and q lines without loops or multiple lines. We write ν(n, q) for the number of smooth (n, q) graphs, i.e. connected graphs without end points, and ν = V(Z, Y) = ∑n,q ν(n,q)ZnYq /n! for the exponential generating function of ν(n,q). We use the Riddell “core and mantle” method to find an explicit form for V (not, as usual with this method, only a functional equation). From this we deduce a partial differential equation satisfied by V. We interpret this equation in purely combinatorial terms. We write Vk = ∑ n ν(n, n + k)Xn/n! and find a recurrence formula for Vk for successive k. We use these and other results to find an asymptotic expansion for ν(n,q) as n→∞ when (q/n) − 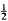 log n −
log n − 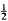 log log n→ + ∞ and an asymptotic approximation to ν(n,n + k) when 0 < k = o
log log n→ + ∞ and an asymptotic approximation to ν(n,n + k) when 0 < k = o and to log ν(n, n + k) when k <
and to log ν(n, n + k) when k <  (1−ε).
(1−ε).
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 91 , Issue 3-4 , 1982 , pp. 205 - 212
- Copyright
- Copyright © Royal Society of Edinburgh 1982
References
- 4
- Cited by


