Published online by Cambridge University Press: 18 April 2018
We show how to deform a metric of the form g = gr + dr2 to a metric 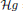 = Hr + dr2, which is a hyperbolic metric for r less than some fixed λ, and coincides with g for r large. Here by hyperbolic metric we mean a metric of constant sectional curvature equal to -1. We study the extent to which
= Hr + dr2, which is a hyperbolic metric for r less than some fixed λ, and coincides with g for r large. Here by hyperbolic metric we mean a metric of constant sectional curvature equal to -1. We study the extent to which 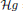 is close to hyperbolic everywhere, if we assume g is close to hyperbolic. A precise definition of the close to hyperbolic concept is given. We also deal with a one-parameter version of this problem. The results in this paper are used in the problem of smoothing Charney–Davis strict hyperbolizations.
is close to hyperbolic everywhere, if we assume g is close to hyperbolic. A precise definition of the close to hyperbolic concept is given. We also deal with a one-parameter version of this problem. The results in this paper are used in the problem of smoothing Charney–Davis strict hyperbolizations.