Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T19:24:33.376Z Has data issue: false hasContentIssue false
  • English
  • Français

Compactness and single-point blowup of positive solutions on bounded domains

Published online by Cambridge University Press:  14 November 2011

Stathis Filippas  and
Frank Merle
Stathis Filippas
Affiliation:
Université Cergy-Pontoise, Département de Mathematique, Avenue du Parc, 8 Le Campus, 95003 Cergy-Pontoise Cedex, France
Frank Merle
Affiliation:
Université Cergy-Pontoise, Département de Mathématique, Avenue du Pare, 8 Le Campus, 95003 Cergy-Pontoise Cedex, France and Université Paris VI, Lab. d'Analyse Numérique, 4, Place Jussieu, 75252 Cedex 05, France
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper is concerned with the blowup of positive solutions of the semilinear heat equation

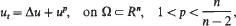
with zero boundary conditions. The domain Ω is supposed to be smooth, convex and bounded. We first show that, under the assumption that the initial data are uniformly monotone near the boundary, solutions that exist on the time interval (0, T form a compact family in a suitable topology. We then derive some localisation properties of these solutions. In particular, we discuss a general criterion, independent of the initial data, which in some cases ensures single-point blowup.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 127 , Issue 1 , 1997 , pp. 47 - 65
Copyright
Copyright © Royal Society of Edinburgh 1997

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Angenent, S.. The zeroset of a solution of a parabolic equation. J. Reine Angew. Math. 390 (1988), 79–96Google Scholar
2Bricmont, J. and Kupiainen, A.. Universality in blowup for nonlinear heat equations. Nonlinearity 7 (1994), 539–75.CrossRefGoogle Scholar
3Chen, X.-Y. and Matano, H.. Convergence, asymptotic periodicity, and finite-point blowup in onedimensional semilinear heat equations. J. Differential Equations 78 (1989), 160–90.CrossRefGoogle Scholar
4Folland, G. B.. Introduction to Partial Differential Equations (Princeton, NJ: Princeton University Press, 1976).CrossRefGoogle Scholar
5Friedman, A.. Partial Differential Equations of Parabolic Type (Englewood Cliffs, NJ: Prentice-Hall, 1964).Google Scholar
6Friedman, A. and McLeod, B.. Blowup of positive solutions of semilinear heat equations. Indiana Univ. Math. J. 34 (1985), 425–47.CrossRefGoogle Scholar
7Gidas, B., Ni, W.-N. and Niremberg, L.. Symmetry and related properties via the maximum principle. Comm. Math. Phys. 68 (1979), 209–43.CrossRefGoogle Scholar
8Giga, Y.. Solutions for semilinear parabolic equations in Lp and regularity of weak solutions of the Navier-Stokes System. J. Differential Equations 68 (1986), 186–212.CrossRefGoogle Scholar
9Giga, Y. and Kohn, R. V.. Asymptotically self similar blowup of semilinear heat equations. Comm. Pure Appl. Math. 38 (1985), 297–319.CrossRefGoogle Scholar
10Giga, Y. and Kohn, R. V.. Characterising blow up using similarity variables. Indiana Univ. Math. J. 36 (1987), 1–40.CrossRefGoogle Scholar
11Giga, Y. and Kohn, R. V.. Nondegeneracy of blowup for semilinear heat equations. Comm. Pure Appl. Math. 42(1989), 845–84.CrossRefGoogle Scholar
12Herrero, M. A. and Velázquez, J. J. L.. Flat blow-up in one-dimensional semilinear parabolic equations. Differential Integral Equations 5 (1992), 973–87.CrossRefGoogle Scholar
13Herrero, M. A. and Velázquez, J. J. L.. Blow-up behaviour of one-dimensional semilinear parabolic equations. Ann. Inst. H. Poincaré, Anal. Non Linéaire 10 (1993), 131–89.CrossRefGoogle Scholar
14Herrero, M. A. and Velázquez, J. J. L.. Some results on blowup for semilinear parabolic problems (IMA Preprint 1000).Google Scholar
15Herrero, M. A. and Velázquez, J. J. L.. Generic behavior of higher dimensional blowup patterns (in prep.).Google Scholar
16Ladyzenskaja, O. A., Solonnikov, V. A. and Ural'ceva, N. N.. Linear and Quasilinear Equations of Parabolic Type, Translations of Mathematical Monographs 23 (Providence, RI: American Mathematical Society, 1968).CrossRefGoogle Scholar
17Levine, H. A.. Some nonexistence and instability theorems for solutions of formally parabolic equations of the form Pu 1 = Au + F(u). Arch. Rational Mech. Anal. 51 (1973), 371–86.CrossRefGoogle Scholar
18Merle, F.. Solution of a nonlinear heat equation with arbitrarily given blowup points. Comm. Pure Appl. Math. 40 (1992), 263–300.CrossRefGoogle Scholar
19Mueller, C. and Weissler, F.. Single point blow up for a general semilinear heat equation. Indiana Univ. Math. J. 34 (1985), 881–913.CrossRefGoogle Scholar
20Ni, W.-M., Sacks, P. E. and Tavantzis, J.. On the asymptotic behavior of solutions of certain quasilinear parabolic equations. J. Differential Equations 54 (1984), 97–120.CrossRefGoogle Scholar
21Velázquez, J. J. L.. Higher dimensional blowup for semilinear parabolic equations. Comm. Partial Differential Equations 17 (1992), 1567–96.CrossRefGoogle Scholar
22Velázquez, J. J. L.. Estimates on the (N — 1 (-dimensional Hausdorff measure of the blow-up set for asemilinear heat equation. Indiana Univ. Math. J. 42 (1993), 445–76.CrossRefGoogle Scholar
23Velázquez, J. J. L.. Local behavior near blowup points for semilinear parabolic equations. J. Differential Equations 106 (1993), 384–415.CrossRefGoogle Scholar
24Weissler, F.. Local existence and nonexistence for semilinear parabolic equations in L p. Indiana Univ. Math.J. 29(1980), 97–102.CrossRefGoogle Scholar
25Weissler, F.. Single point blowup for a semilinear initial value problem. J. Differential Equations 55 (1984), 204–24.CrossRefGoogle Scholar