Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-24T05:31:52.118Z Has data issue: false hasContentIssue false
  • English
  • Français

Coarse fundamental groups and box spaces

Part of: Special aspects of infinite or finite groups Structure and classification of infinite or finite groups

Published online by Cambridge University Press:  30 January 2019

Thiebout Delabie  and
Ana Khukhro
Thiebout Delabie
Affiliation:
Institut de Mathématiques, Université de Neuchâtel, Switzerland ([email protected])
Ana Khukhro
Affiliation:
Institut de Mathématiques, Université de Neuchâtel, Switzerland ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We use a coarse version of the fundamental group first introduced by Barcelo, Kramer, Laubenbacher and Weaver to show that box spaces of finitely presented groups detect the normal subgroups used to construct the box space, up to isomorphism. As a consequence, we have that two finitely presented groups admit coarsely equivalent box spaces if and only if they are commensurable via normal subgroups. We also provide an example of two filtrations (Ni) and (Mi) of a free group F such that Mi > Ni for all i with [Mi:Ni] uniformly bounded, but with 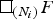$\squ _{(N_i)}F$ not coarsely equivalent to 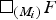$\squ _{(M_i)}F$. Finally, we give some applications of the main theorem for rank gradient and the first ℓ2 Betti number, and show that the main theorem can be used to construct infinitely many coarse equivalence classes of box spaces with various properties.

Keywords

Coarse geometrycoarse fundamental groupbox spaces

MSC classification

Primary: 20F69: Asymptotic properties of groups
Secondary: 20F34: Fundamental groups and their automorphisms 20E26: Residual properties and generalizations; residually finite groups 20F65: Geometric group theory
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 150 , Issue 3 , June 2020 , pp. 1139 - 1154
Copyright
Copyright © 2019 The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Abért, M., Jaikin-Zapirain, A. and Nikolov, N.. The rank gradient from a combinatorial viewpoint. Groups Geom. Dyna. 5 (2011), 213–230.CrossRefGoogle Scholar
2Alekseev, V. and Finn-Sell, M.. Sofic boundaries of groups and coarse geometry of sofic approximations, preprint, arxiv:1608.02242 (2016)Google Scholar
3Babson, E., Barcelo, H., de Longueville, M. and Laubenbacher, R.. Homotopy theory of graphs. J. Alg. Comb. 24 (2006), 31–44.CrossRefGoogle Scholar
4Barcelo, H. and Laubenbacher, R.. Perspectives in A-homotopy theory and its applications Discrete Mathematics. 298 (2005), 39–61.CrossRefGoogle Scholar
5Barcelo, H., Kramer, X., Laubenbacher, R. and Weaver, C.. Foundations of a connectivity theory for simplicial complexes. Advances in Applied Math. 26 (2001), 97–128.CrossRefGoogle Scholar
6Barcelo, H., Capraro, V. and White, J. A.. Discrete homology theory for metric spaces. Bull. Lond. Math. Soc. 46 (2014), 889–905.CrossRefGoogle Scholar
7Chen, X., Wang, Q. and Wang, X.. Characterization of the Haagerup property by fibred coarse embedding into Hilbert space. Bull. Lond. Math. Soc. 45 (2013), 1091–1099.CrossRefGoogle Scholar
8Das, K.. From the geometry of box spaces to the geometry and measured couplings of groups, arXiv:1512.08828 (2015).Google Scholar
9Delabie, T. and Khukhro, A.. Box spaces of the free group that neither contain expanders nor embed into a Hilbert space, preprint, arXiv:1611.08451 (2016).Google Scholar
10Hatcher, A.. Algebraic topology (Cambridge: Cambridge University Press, 2002).Google Scholar
11Hume, D.. A continuum of expanders. Fund. Math. 238 (2017), 143–152.CrossRefGoogle Scholar
12Khukhro, A.. Box spaces, group extensions and coarse embeddings into Hilbert space. J. Funct. Anal. 263 (2012), 115–128.CrossRefGoogle Scholar
13Khukhro, A.. Embeddable box spaces of free groups. Math. Ann. 360 (2014), 53–66.CrossRefGoogle Scholar
14Khukhro, A. and Valette, A.. Expanders and box spaces, preprint, arXiv:1509.01394 (2015).Google Scholar
15Lackenby, M.. Expanders, rank and graphs of groups. Israel J. Math. 146 (2005), 357–370.CrossRefGoogle Scholar
16Lubotzky, A.. Discrete groups, expanding graphs and invariant measures. Birkhäuser Progress in Mathematics 125 (1994).Google Scholar
17Lück, W.. Approximating L2-invariants by their finite-dimensional analogues. Geom. Funct. Anal. 4 (1994), 455–481.CrossRefGoogle Scholar
18Lück, W.. L2-invariants: theory and applications to geometry and K-theory, Ergebnisse der Mathematik und ihrer Grenzgebiete (3 Series), vol. 44 (Heidelberg, Berlin: Springer-Verlag, 2002).CrossRefGoogle Scholar
19Margulis, G.. Explicit constructions of expanders. Prob. Pered. Inform. 9 (1973), 71–80.Google Scholar
20Nowak, P. and Yu, G.. Large scale geometry. EMS Textbooks in Mathematics, EMS (2012).Google Scholar
21Roe, J.. Lectures on Coarse Geometry, AMS University Lecture Series 31, AMS (2003).CrossRefGoogle Scholar
22Willett, R. and Yu, G.. Higher index theory for certain expanders and Gromov monster groups II. Adv. Math. 229 (2012), 1762–1803.CrossRefGoogle Scholar